(本小题满分12分)已知数列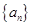 的前
的前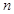 项和为
项和为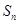 ,
,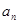 .
.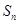 满足
满足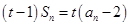 (
(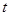 为常数,
为常数,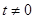 且
且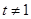 ).
).
(1)求数列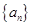 的通项公式;
的通项公式;
(2)设 ,当
,当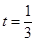 时,求数列
时,求数列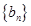 的前
的前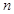 项和
项和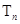 .
.
数列{an}是首项a1=4的等比数列,且S3,S2,S4成等差数列.
(1)求数列{an}的通项公式;
(2)设bn=log2|an|,Tn为数列 的前n项和,求Tn.
的前n项和,求Tn.
已知数列{an}的前n项和为Sn,且a1=1,nan+1=(n+2)Sn (n∈N*).
(1)求证:数列 为等比数列;
为等比数列;
(2)求数列{an}的通项公式及前n项和Sn;
(3)若数列{bn}满足:b1= ,
, =
= (n∈N*),求数列{bn}的通项公式.
(n∈N*),求数列{bn}的通项公式.
已知Sn是数列{an}的前n项和,且an=Sn-1+2(n≥2),a1=2.
(1)求数列{an}的通项公式;
(2)设bn= ,Tn=bn+1+bn+2+…+b2n,是否存在最大的正整数k,使得对于任意的正整数n,有Tn>
,Tn=bn+1+bn+2+…+b2n,是否存在最大的正整数k,使得对于任意的正整数n,有Tn> 恒成立?若存在,求出k的值;若不存在,说明理由.
恒成立?若存在,求出k的值;若不存在,说明理由.
将函数f(x)=sin x·sin
x·sin (x+2
(x+2 )·sin
)·sin (x+3
(x+3 )在区间(0,+∞)内的全部极值点按从小到大的顺序排成数列{an} (n=1,2,3,…).
)在区间(0,+∞)内的全部极值点按从小到大的顺序排成数列{an} (n=1,2,3,…).
(1)求数列{an}的通项公式;
(2)设bn=sinansinan+1sinan+2,求证:bn= (n=1,2,3,…).
(n=1,2,3,…).
设等差数列{an}的首项a1及公差d都为整数,前n项和为Sn.
(1)若a11=0,S14=98,求数列{an}的通项公式;
(2)若a1≥6,a11>0,S14≤77,求所有可能的数列{an}的通项公式.