(本小题满分14分)已知椭圆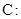
 (
(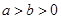 )的离心率为
)的离心率为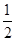 ,点
,点 在椭圆
在椭圆 上,
上,
过椭圆 的右焦点的动直线
的右焦点的动直线 与椭圆
与椭圆 相交于
相交于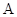 、
、 两点.
两点.
(1)求椭圆 的标准方程;
的标准方程;
(2)若线段 中点的横坐标为
中点的横坐标为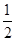 ,求直线
,求直线 的方程;
的方程;
(3)若线段 的垂直平分线与
的垂直平分线与 轴相交于点
轴相交于点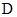 .设弦
.设弦 的中点为
的中点为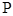 ,试求
,试求 的取值范围.
的取值范围.
已知椭圆的长轴长为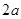 ,焦点是
,焦点是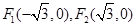 ,点
,点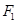 到直线
到直线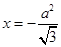 的距离为
的距离为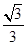 ,过点
,过点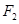 且倾斜角为锐角的直线
且倾斜角为锐角的直线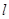 与椭圆交于A、B两点,使得|
与椭圆交于A、B两点,使得|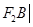 =3|
=3|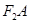
 .
.
(1)求椭圆的标准方程;
(2)求直线l的方程.
设函数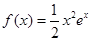 .
.
(1)求f(x)的单调区间;
(2)若当x∈[-2,2]时,不等式f(x)>m恒成立,求实数m的取值范围.
在极坐标系中,已知圆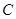 经过点
经过点 ,圆心为直线
,圆心为直线 与极轴的交点,求圆
与极轴的交点,求圆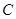 的极坐标方程.
的极坐标方程.
在直角坐标系中,以原点为极点, 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线
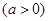 ,过点
,过点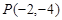 的直线
的直线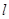 的参数方程为:
的参数方程为:
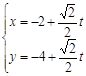 ,(t为参数),直线
,(t为参数),直线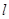 与曲线
与曲线 分别交于
分别交于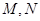 两点.
两点.
(1)写出曲线 和直线
和直线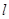 的普通方程;
的普通方程;
(2)若 成等比数列,求
成等比数列,求 的值.
的值.
已知函数 .
.
(1)当 时,求函数
时,求函数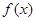 的定义域;
的定义域;
(2)若关于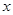 的不等式
的不等式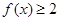 的解集是
的解集是 ,求
,求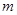 的取值范围.
的取值范围.