（本小题满分12分）某校在一次对是否喜欢英语学科的学生的抽样调查中，随机抽取了100名同学，相关的数据如下表所示：
| |
不喜欢英语 |
喜欢英语 |
总计 |
| 男生 |
40 |
18 |
58 |
| 女生 |
15 |
27 |
42 |
| 总计 |
55 |
45 |
100 |
（Ⅰ）试运用独立性检验的思想方法分析：是否有99 %的把握认为“学生是否喜欢英语与性别有关？”说明理由．
（Ⅱ）用分层抽样方法在喜欢英语学科的学生中随机抽取5名，女学生应该抽取几名？
（Ⅲ）在上述抽取的5名学生中任取2名，求恰有1名学生为男性的概率．
附：
=
，
 |
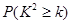0．100 |
0．050 |
0．025 |
0．01 |
0．001 |
 |
2．706 |
3．841 |
5．024 |
6．635 |
10．828 |
已知圆的参数方程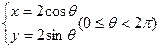
（1）设
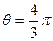时对应的点这P，求直线OP的倾斜角；（2）若此圆经过点（m,1），求m的值，其中
；（3）求圆上点到直线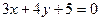
距离的最值．
．要将甲、乙两种长短不同的钢管截成A、B、C三种规格，每根钢管可同时截得三种规格的短钢管的根数如下表所示：
规格类型
|
A规格 |
B规格 |
C规格 |
||
| 甲种钢管 |
2 |
1 |
4 |
||
| 乙种钢管 |
2 |
3 |
1 |
今需A、B、C三种规格的钢管各13、16、18根，问各截这两种钢管多少根可得所需三种规格钢管，且使所用钢管根数
已知圆的半径为
，圆心在直线
上，圆被直线
截得的弦长为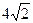
，求圆的方程．
过点P(2,4)作两条互相垂直的直线l１，l２，若l１交x轴于A点，
l2 交y轴于B点，求线段AB的中点M的轨迹方程． 
求经过两点P1（2，1）和P2（m，2）（m∈R)的直线l的斜率，并且求出l的倾斜角α及其取值范围．