如图,已知AB∥CD,∠1:∠2:∠3=1:2:3,求证:BA平分∠EBF.
下面给出证法1.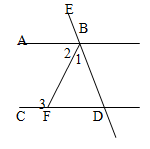
证法1:∠1、∠2、∠3的度数分别为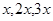 ,
,
∵AB∥CD,∴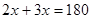 °,解得
°,解得 ,
,
∴∠1=36°,∠2=72°,∠3=108°,
∵∠EBD=180°,∴∠EBA=72°,
∴BA平分∠EBF.
请阅读证法1后,找出与证法1不同的证法2,并写出证明过程.
在一次数学测验活动中,小明到操场测量旗杆AB的高度,他手拿一支铅笔MN,边观察边移动(铅笔MN始终与地面垂直)。如示意图,当小明移动到D点时,眼睛C与铅笔、旗杆的顶端M、A共线,同时,眼睛C与它们的底端N、B也恰好共线。此时,测得DB=50m,小明的眼睛C到铅笔的距离为0.65m,铅笔MN的长为0.16m,请你帮助小明计算出旗杆AB的高度(结果精确到0.1m)。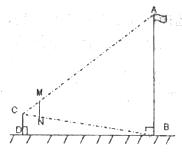
如图所示在平行四边形ABCD中,E是CD的延长线上一点,BE与AD交于点F,DE= CD.
CD.
(1)求证:△ABF∽△CEB;
(2)若S△DEF面积为2,求S平行四边形ABCD的面积。
已知 ,求
,求 。
。
在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共20只,某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复,表是活动进行中的一组统计数据:
| 摸球的次数n |
100 |
150 |
200 |
500 |
800 |
1000 |
| 摸到白球的次数m |
68 |
109 |
136 |
345 |
368 |
701 |
| 摸到乒乓球的频率 |
0.68 |
0.73 |
0.68 |
0.69 |
0.70 |
0.70 |
(1)请估计:当n很大时,摸到白球的频率将会接近________;
(2)假如你去摸一次,你摸到白球的概率是_______,摸到黑球的概率是_______;
(3)试估算口袋中黑、白两种颜色的球各有多少只?
如图,正方形ABCD中,E、F分别是AB、BC边上的点,且AE=BF,求证:AF⊥DE。