本题共有2个小题,第(1)小题满分4分,第(2)小题满分10分.
设三角形 的内角
的内角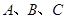 所对的边长分别是
所对的边长分别是 ,且
,且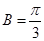 .若
.若 不是钝角三角形,求:
不是钝角三角形,求:
(1)角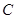 的范围;
的范围;
(2) 的取值范围.
的取值范围.
设数列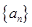 的前
的前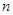 项和为
项和为 ,点
,点 均在函数
均在函数 的图象上.
的图象上.
(Ⅰ)求数列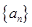 的通项公式;
的通项公式;
(Ⅱ)若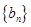 为等比数列,且
为等比数列,且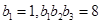 ,求数列
,求数列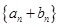 的前
的前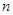 项和
项和 .
.
已知函数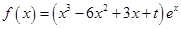 (
(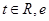 为自然对数的底数)
为自然对数的底数)
(Ⅰ)若函数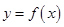 有三个极值点,求
有三个极值点,求 的取值范围
的取值范围
(Ⅱ)若存在实数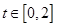 ,使对任意的
,使对任意的 ,不等式
,不等式 恒成立,求正整数
恒成立,求正整数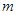 的最大值.
的最大值.
椭圆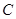 的中心为坐标原点
的中心为坐标原点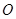 ,焦点在
,焦点在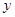 轴上,短轴长为
轴上,短轴长为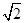 、离心率为
、离心率为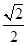 ,直线
,直线 与
与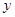 轴交于点
轴交于点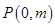 ,与椭圆
,与椭圆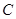 交于相异两点
交于相异两点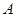 、
、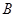 ,且
,且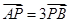 .
.
(Ⅰ)求椭圆方程;(Ⅱ)求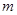 的取值范围.
的取值范围.
设甲、乙、丙三个乒乓球协会的运动员人数分别为27,9,18,先采用分层抽样的方法从这三个协会中抽取6名运动员参加比赛.
(Ⅰ)求应从这三个协会中分别抽取的运动员人数;
(Ⅱ)将抽取的6名运动员进行编号,编号分别为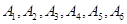 ,从这6名运动员中随机抽取2名参加双打比赛.
,从这6名运动员中随机抽取2名参加双打比赛.
(ⅰ)用所给编号列出所有可能的结果;
(ⅱ)设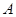 为事件“编号为
为事件“编号为 的两名运动员至少有一人被抽到”,求事件
的两名运动员至少有一人被抽到”,求事件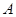 发生的概率.
发生的概率.
如图1,平面四边形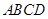 关于直线
关于直线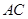 对称,
对称,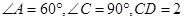 ,把
,把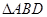 沿
沿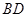 折起(如图2),使二面角
折起(如图2),使二面角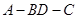 为直二面角.
为直二面角.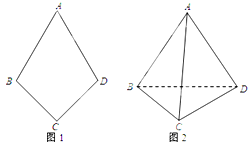
(Ⅰ)求 与平面
与平面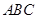 所成的角的余弦值;
所成的角的余弦值;
(Ⅱ)求二面角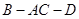 的大小的正弦值.
的大小的正弦值.