在直角梯形PBCD中A为PD的中点,如下左图。 ,将
,将 沿AB折到
沿AB折到 的位置,使
的位置,使 ,点E在SD上,且
,点E在SD上,且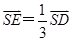 ,如下右图。
,如下右图。
(1)求证: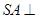 平面ABCD;
平面ABCD;
(2)求二面角E—AC—D的正切值.
已知定义域为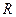 的函数
的函数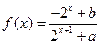 是奇函数.
是奇函数.
(1)求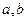 的值;
的值;
(2)若对任意的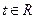 ,不等式
,不等式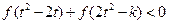 恒成立,求
恒成立,求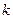 的取值范围;
的取值范围;
设二次函数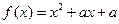 ,方程
,方程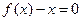 的两根
的两根 和
和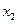 满足
满足 .
.
(Ⅰ)求实数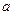 的取值范围;
的取值范围;
(Ⅱ)试比较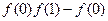 与
与 的大小.并说明理由.
的大小.并说明理由.
设等比数列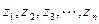 ,其中
,其中 ,
, ,
,
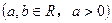 .(1)求
.(1)求 ,
, 的值.
的值.
(2)求使 的最小正整数
的最小正整数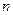 的值.
的值.
某农场种植火龙果的成本x(单位:万元)与收益y(单位:万元)之间关系如下:
| x |
2 |
4 |
6 |
8 |
10 |
| Y |
10 |
13 |
15 |
18 |
20 |
(1)假定y与x之间有线性关系,求其线性回归方程。
(2)若收益不少于16万元,则投入的成本不少于多少万元。
(提示:
 )
)
2008年奥运会的一套吉祥物有五个,分别命名:“贝贝”、 “晶晶”、“欢欢”、“迎迎”和“妮妮”,称“奥运福娃”。甲、乙两位小学生各有一套吉祥物,现以投掷一个骰子的方式进行游戏,规则如下:当出现向上的点数是奇数时,甲将赢得乙一个福娃;否则乙赢得甲一个福娃。现规定掷骰子的总次数达9次时,或在此
“晶晶”、“欢欢”、“迎迎”和“妮妮”,称“奥运福娃”。甲、乙两位小学生各有一套吉祥物,现以投掷一个骰子的方式进行游戏,规则如下:当出现向上的点数是奇数时,甲将赢得乙一个福娃;否则乙赢得甲一个福娃。现规定掷骰子的总次数达9次时,或在此 前某学生已赢得所有福娃时游戏终止,记游戏终止时投掷骰子的总次数为
前某学生已赢得所有福娃时游戏终止,记游戏终止时投掷骰子的总次数为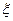 .
.
(1)求掷骰子的次数为7的概率;
(2)求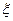 的分布列及数学期望E
的分布列及数学期望E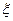 .
.