如图,在菱形ABCD中,AB=2, ,点E是AD边的中点,点M是AB边上一动点(不与点A重合),延长ME交射线CD于点N,连接MD,AN.
,点E是AD边的中点,点M是AB边上一动点(不与点A重合),延长ME交射线CD于点N,连接MD,AN.
(1)求证:四边形AMDN是平行四边形;
(2)填空:①当AM的值为 时,四边形AMDN是矩形;
②当AM的值为 时,四边形AMDN是菱形。
如图,抛物线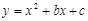 与
与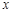 轴交于A(-1,0),B(3,0) 两点.
轴交于A(-1,0),B(3,0) 两点.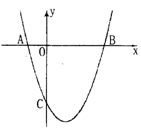
(1) 求该抛物线的解析式;
(2) 设(1)中的抛物线上有一个动点P,当点P在该抛物线上滑动到什么位置时,满足S△PAB=8,并求出此时P点的坐标;
(3) 设(1)中抛物线交y 轴于C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.
如图9-1,9-2,△ABC是等边三角形,D、E分别是AB、BC边上的两个动点(与点A、B、C不重合),始终保持BD=CE.
(1)当点D、E运动到如图9-1所示的位置时,求证:CD=AE.
(2)把图9-1中的△ACE绕着A点顺时针旋转60°到△ABF的位置(如图9-2),分别连结DF、EF.
① 找出图中所有的等边三角形(△ABC除外),并对其中一个给予证明;
② 试判断四边形CDFE的形状,并说明理由
如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点B的坐标为(1,0)。
⑴ 画出△ABC关于 轴对称的△A1B1C1;
轴对称的△A1B1C1;
⑵ 画出将△ABC绕原点O按逆方向旋转 所得的△A2B2C2;
所得的△A2B2C2;
⑶ △A1B1C1与△A2B2C2成轴对称吗?若成轴对称,画出所有的对称轴;
⑷ △A1B1C1与△A2B2C2成中心对称吗?若成中心对称,写出对称中心的坐标。
我市某中学为了丰富校园文化生活,校学生会决定举办演讲、歌唱、绘画、舞蹈四项比赛,要求每位学生都参加,且只能参加一项比赛。围绕“你参赛的项目是什么?(只写一项)”的问题,校学生会在全校范围内随机抽取部分学生进行问卷调查,将调查问卷适合整理后绘制成如图所示的不完整的条形统计图,其中参加舞蹈比赛的人数与参加歌唱比赛的人数之比为1∶3,请你根据以上信息回答下列问题:
⑴ 通过计算补全条形统计图;
⑵ 在这次调查中,一共抽取了多少名学生?
⑶ 如果全校有680名学生,请你估计这680名学生中参加演讲比赛的学生有多少名?
学校组织各班开展“阳光体育”活动,某班体育委员第一次到商店购买了5个毽子和8根跳绳,花费34元,第二次又购买了3个毽子和4根跳绳,花费18元。求每个毽子和每根跳绳各多少元?