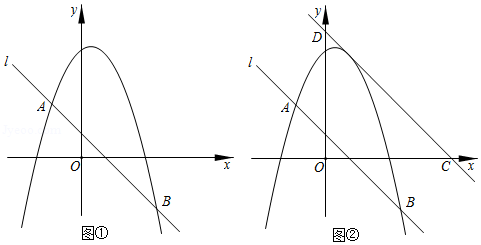
如图(1),在直角坐标系xOy中,抛物线与x轴交于A、B两点,交y轴于点C,过A点的直线与抛物线的另一交点为D(m,3),与y轴相交于点E,点A的坐标为(-1,0),∠BAD=45°,点P是抛物线上的一点,且点P在第一象限.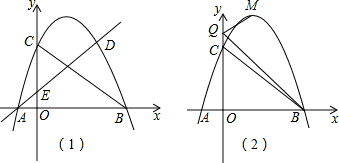
(1)求直线AD和抛物线的解析式;
(2)若S△PBC:S△BOC=2:3,求点P的坐标;
(3)如图(2),若M为抛物线的顶点,点Q为y轴上一点,求使QM+QB最小时,点Q的坐标,并求QM+QB的最小值.
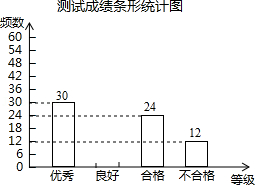
在世界环境日 月5日),学校组织了保护环境知识测试,现从中随机抽取部分学生的成绩作为样本,按“优秀”“良好”“合格”“不合格”四个等级进行统计,绘制了如下尚不完整的统计图表.
测试成绩统计表
|
等级 |
频数(人数) |
频率 |
|
优秀 |
30 |
|
|
良好 |
|
0.45 |
|
合格 |
24 |
0.20 |
|
不合格 |
12 |
0.10 |
|
合计 |
|
1 |
根据统计图表提供的信息,解答下列问题:
(1)表中 , , ;
(2)补全条形统计图;
(3)若该校有2400名学生参加了本次测试,估计测试成绩等级在良好以上(包括良好)的学生约有多少人?
化简 .
解方程组
计算 .
如图①,二次函数 的图象与直线 交于 、 两点.点 是 轴上的一个动点,过点 作 轴的垂线交直线1于点 ,交该二次函数的图象于点 ,设点 的横坐标为 .
(1) , ;
(2)若点 在点 的上方,且 ,求 的值;
(3)将直线 向上平移4个单位长度,分别与 轴、 轴交于点 、 (如图② .
①记 的面积为 , 的面积为 ,是否存在 ,使得点 在直线 的上方,且满足 ?若存在,求出 及相应的 , 的值;若不存在,请说明理由.
②当 时,将线段 绕点 顺时针旋转 得到线段 ,连接 、 、 .若 ,直接写出直线 与该二次函数图象交点的横坐标.