如图,在等腰直角△ABC中,∠ACB=90°,点D、F为BC边上的两点,CD=BF,连接AD,过点C作AD的垂线角AB于点E,连接EF.
(1)若∠DAB=15°,AB=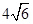 ,求线段AD的长度.
,求线段AD的长度.
(2)求证:∠EFB=∠CDA.
如图,在平面直角坐标系中,直线 与 轴交于点 ,与 轴交于点 ,抛物线 经过坐标原点和点 ,顶点为点 .
(1)求抛物线的关系式及点 的坐标;
(2)点 是直线 下方的抛物线上一动点,连接 , ,当 的面积等于 时,求 点的坐标;
(3)将直线 向下平移,得到过点 的直线 ,且与 轴负半轴交于点 ,取点 ,连接 ,求证: .

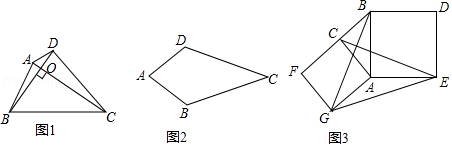
如图1,对角线互相垂直的四边形叫做垂美四边形.
(1)概念理解:如图2,在四边形 中, , ,问四边形 是垂美四边形吗?请说明理由;
(2)性质探究:如图1,垂美四边形 的对角线 , 交于点 .猜想: 与 有什么关系?并证明你的猜想.
(3)解决问题:如图3,分别以 的直角边 和斜边 为边向外作正方形 和正方形 ,连结 , , .已知 , ,求 的长.
如图, 是 的外接圆,点 在 边上, 的平分线交 于点 ,连接 , ,过点 作 的切线与 的延长线交于点 .
(1)求证: ;
(2)求证: ;
(3)当 , 时,求线段 的长.

小明根据学习函数的经验,参照研究函数的过程与方法,对函数 的图象与性质进行探究.
因为 ,即 ,所以可以对比函数 来探究.
列表:(1)下表列出 与 的几组对应值,请写出 , 的值: , ;
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
|
|
|
|
|
|
1 |
2 |
4 |
|
|
|
|
|
|
|
|
|
|
|
2 |
3 |
|
|
|
0 |
|
|
|
描点:在平面直角坐标系中,以自变量 的取值为横坐标,以 相应的函数值为纵坐标,描出相应的点,如图所示:

(2)请把 轴左边各点和右边各点,分别用条光滑曲线顺次连接起来;
(3)观察图象并分析表格,回答下列问题:
①当 时, 随 的增大而 ;(填“增大”或“减小”
②函数 的图象是由 的图象向 平移 个单位而得到.
③函数图象关于点 中心对称.(填点的坐标)
2020年7月23日,我国首次火星探测"天问一号"探测器,由长征五号遥四运载火箭在中国文昌航天发射场发射成功,正式开启了中国的火星探测之旅.运载火箭从地面 处发射,当火箭到达点 时,地面 处的雷达站测得 米,仰角为 秒后,火箭直线上升到达点 处,此时地面 处的雷达站测得 处的仰角为 . , , 在同一直线上,已知 , 两处相距460米,求火箭从 到 处的平均速度.(结果精确到1米,参考数据: ,
