(本小题满分14分)已知点
 在直线
在直线 :
: 上,
上,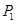 是直线
是直线 与
与 轴的
轴的
交点,数列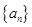 是公差为1的等差数列.
是公差为1的等差数列.
(1)求数列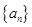 ,
,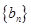 的通项公式;
的通项公式;
(2)若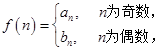 是否存在
是否存在 ,使
,使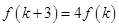 成立?若存在,求出所有符合
成立?若存在,求出所有符合
条件的 值;若不存在,请说明理由.
值;若不存在,请说明理由.
已知等差数列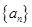 满足:
满足: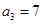 ,
,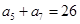 ,
,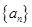 的前n项和为
的前n项和为 .
.
(Ⅰ)求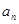 及
及 ;
;
(Ⅱ)令bn=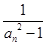 (n
(n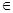 N*),求数列
N*),求数列 的前n项和
的前n项和 .
.
(本小题满分10分)选修4-5:不等式选修
在 ,
,
 的前提下,求a的一个值,是它成为
的前提下,求a的一个值,是它成为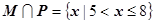 的一个充分但不必要条件。
的一个充分但不必要条件。
(本小题满分10分)选修4-4:坐标系与参数方程已知曲线C的极坐标方程是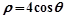 .以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线l的参数方程是:
.以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线l的参数方程是: (
( 是参数).
是参数).
(1)将曲线C的极坐标方程和直线 参数方程转化为普通方程;
参数方程转化为普通方程;
(2)若直线l与曲线C相交于A、B两点,且 ,试求实数
,试求实数 值.
值.
(本小题满分10分)选修4-1:几何证明讲 如图,AB是⊙O的直径,弦BD、CA的延长线相交于点E,EF垂直BA的延长线于点F. 
求证:(1)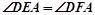 ;
;
(2)AB2=BE•BD-AE•AC.
(本小题满分12分)
若函数 的定义域为
的定义域为 ,其中a、b为任
,其中a、b为任
意正实数,且a<b。
(1)当A= 时,研究
时,研究 的单调性(不必证明);
的单调性(不必证明);
(2)写出 的单调区间(不必证明),并求函数
的单调区间(不必证明),并求函数 的最小值、最大值;
的最小值、最大值;
(3)若 其中k是正整数,对一切正整数k不等式
其中k是正整数,对一切正整数k不等式 都有解,求m的取值范围。
都有解,求m的取值范围。