(本小题满分10分)选修4—1:几何证明选讲
如图, 内接于直径为
内接于直径为 的圆
的圆 ,过点
,过点 作圆
作圆 的切线交
的切线交 的延长线于点
的延长线于点 ,
, 的平分线分别交
的平分线分别交 和圆
和圆 于点
于点 ,若
,若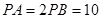 .
.
(1)求证: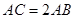 ;
;
(2)求 的值.
的值.
已知函数f(x)=ex+2x2—3x
(1)求曲线y=f(x)在点(1,f(1))处的切线方程;
(2) 当x ≥1时,若关于x的不等式f(x)≥ax恒成立,求实数a的取值范围;
(3)求证函数f(x)在区间[0,1)上存在唯一的极值点,并用二分法求函数取得极值时相应x的近似值(误差不超过0.2);(参考数据e≈2.7, ≈1.6,e0.3≈1.3)。
≈1.6,e0.3≈1.3)。
已知a,b均为正数,且a+b=1,证明:
(1)
(2)
在平面直角坐标系 中,原点为
中,原点为 ,抛物线
,抛物线 的方程为
的方程为 ,线段
,线段 是抛物线
是抛物线 的一条动弦.
的一条动弦.
(1)求抛物线 的准线方程和焦点坐标
的准线方程和焦点坐标 ;
;
(2)若 ,求证:直线
,求证:直线 恒过定点;
恒过定点;
(3)当 时,设圆
时,设圆 ,若存在且仅存在两条动弦
,若存在且仅存在两条动弦 ,满足直线
,满足直线 与圆
与圆 相切,求半径
相切,求半径 的取值范围?
的取值范围?
定义函数 (
( 为定义域)图像上的点到坐标原点的距离为函数的
为定义域)图像上的点到坐标原点的距离为函数的 的模.若模存在最大值,则称之为函数
的模.若模存在最大值,则称之为函数 的长距;若模存在最小值,则称之为函数
的长距;若模存在最小值,则称之为函数 的短距.
的短距.
(1)分别判断函数 与
与 是否存在长距与短距,若存在,请求出;
是否存在长距与短距,若存在,请求出;
(2)求证:指数函数 的短距小于1;
的短距小于1;
(3)对于任意 是否存在实数
是否存在实数 ,使得函数
,使得函数 的短距不小于2,若存在,请求出
的短距不小于2,若存在,请求出 的取值范围;不存在,则说明理由?
的取值范围;不存在,则说明理由?
数列 的首项
的首项 ,
,
求数列 的通项公式;
的通项公式;
设 的前
的前 项和为
项和为 ,求
,求 的最小值.
的最小值.