已知直角△ABC中,周长为L,面积为S,求证:4S≤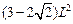 .
.
(本题满分12分)
已知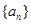 是一个公差大于
是一个公差大于 的等差数列,且满足
的等差数列,且满足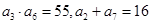 .数列
.数列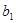 ,
,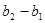 ,
,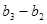 ,…,
,…,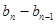 是首项为
是首项为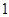 ,公比为
,公比为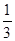 的等比数列.
的等比数列.
(1) 求数列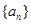 的通项公式;
的通项公式;
(2) 若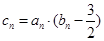 ,求数列
,求数列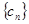 的前
的前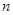 项和
项和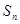 .
.
(本题满分12分)
某风景区有40辆自行车供游客租赁使用,管理这些自行车的费用是每日72元。根据经验,若每辆自行车的日租金不超过6元,则自行车可以全部租出;若超出6元,则每超过1元,租不出的自行车就增加3辆。为了便于结算,每辆自行车的日租金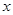 (元)只取整数,并且要求出租自行车一日的总收入必须高于这一日的管理费用,用
(元)只取整数,并且要求出租自行车一日的总收入必须高于这一日的管理费用,用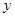 (元)表示出租自行车的日净收入(即一日中出租自行车的总收入减去管理费用后的所得)。
(元)表示出租自行车的日净收入(即一日中出租自行车的总收入减去管理费用后的所得)。
(1)求函数 的解析式及其定义域;
的解析式及其定义域;
(2)试问当每辆自行车的日租金定为多少元时,才能使一日的净收入最多?
(本题满分12分)
在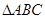 中,角
中,角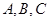 所对的边分别为
所对的边分别为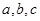 ,且满足
,且满足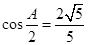 ,
,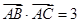 .
.
(1)求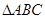 的面积;
的面积;
(2)若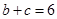 ,求
,求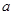 的值.
的值.
(本题满分12分)
已知集合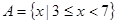 ,
,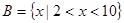 ,
,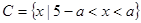 .
.
(1)求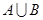 ,
, 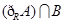 ;
;
(2)若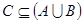 ,求
,求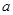 的取值范围.
的取值范围.
(本小题满分14分)
已知函数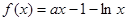
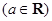 .
.
(1)讨论函数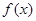 在定义域内的极值点的个数;
在定义域内的极值点的个数;
(2)若函数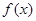 在
在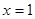 处取得极值,对
处取得极值,对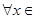
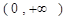 ,
,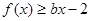 恒成立,
恒成立,
求实数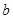 的取值范围;
的取值范围;
(3)当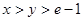 时,求证:
时,求证: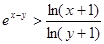 .
.