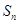本题共有2小题,第(1)小题满分6分,第(2)小题满分8分.
为了在夏季降温和冬季供暖时减少能源损耗,房屋的屋顶和外墙需要建造隔热层.某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元.该建筑物每年的能源消耗费用 (单位:万元)与隔热层厚度
(单位:万元)与隔热层厚度 (单位:cm)满足关系:
(单位:cm)满足关系:
 ,若不建隔热层,每年能源消耗费用为8万元,设
,若不建隔热层,每年能源消耗费用为8万元,设 为隔热层建造费用与20年的能源消耗费用之和.
为隔热层建造费用与20年的能源消耗费用之和.
(1)求 的值及
的值及 的表达式;
的表达式;
(2)隔热层修建多厚时,总费用 达到最小,并求最小值.
达到最小,并求最小值.
如图,山脚下有一小塔AB,在塔底B测得山顶C的仰角为60°,在山顶C测得塔顶A的俯角为45°,已知塔高AB=20 m,求山高CD.
数列{an}的首项为3,{bn}为等差数列且bn=an+1-an(n∈N*).若b3=-2,b10=12,求a8的值
已知函数y= cos2x+
cos2x+ sinxcosx+1,x∈R.
sinxcosx+1,x∈R.
(1)当函数y取得最大值时,求自变量x的集合;
(2)求该函数的的单调增区间
设各项均为正数的等比数列{an}中,a1+a3=10,a3+a5=40. 数列{bn}中,前n项和
(1)求数列{an}与{bn}的通项公式;
(2)若c1=1,cn+1=cn+ ,求数列
,求数列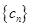 的通项公式
的通项公式
(3)是否存在正整数k,使得 +
+ +…+
+…+ >
>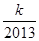 对任意正整数n均成立?若存在,求出k的最大值,若不存在,说明理由.
对任意正整数n均成立?若存在,求出k的最大值,若不存在,说明理由.
某企业在第1年初购买一台价值为120万元的设备M,M的价值在使用过程中逐年减少.从第2年到第6年,每年初M的价值比上年初减少10万元;从第7年开始,每年初M的价值为上年初的75%.
(1)求第n年初M的价值an的表达式;
(2)求数列 的前n项和
的前n项和