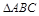 与
与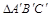 在平面直角坐标系中的位置如图.
在平面直角坐标系中的位置如图.
(1)分别写出下列各点的坐标: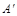 ;
;  ;
;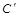 ;
;
(2)说明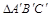 由
由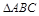 经过怎样的平移得到? .
经过怎样的平移得到? .
(3)若点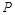 (
( ,
, )是
)是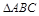 内部一点,则平移后
内部一点,则平移后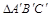 内的对应点
内的对应点 的坐标为 ;
的坐标为 ;
(4)求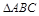 的面积.
的面积.
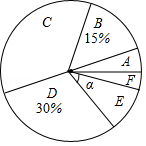
在疫情期间,为落实“停课不停学”,某校对本校学生某一学科在家学习情况进行抽样调查,了解到学生的学习方式有:电视直播、任课教师在线辅导、教育机构远程教学、自主学习.参与调查的学生只能选择一种学习方式,将调查结果绘制成不完整的扇形统计图和条形统计图.根据如图所示的统计图,解答下列问题.
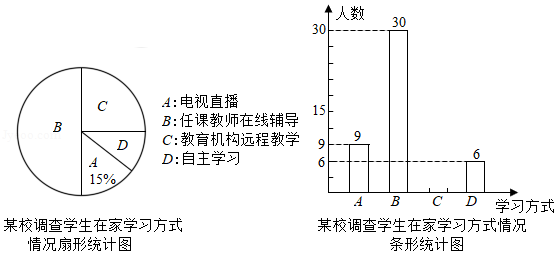
(1)本次接受调查的学生有 名;
(2)补全条形统计图;
(3)根据调查结果,若本校有1800名学生,估计有多少名学生参与任课教师在线辅导?
如图,在 中,点 是边 的中点,连结 并延长到点 ,使 ,连结 .
(1)求证: ;
(2)若 的面积为5,求 的面积.

(1)计算: ;
(2)化简: .
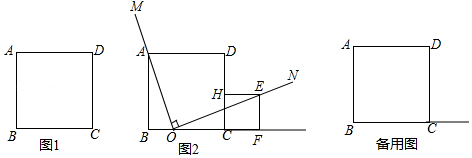
正方形 的边长为1,点 是 边上的一个动点(与 , 不重合),以 为顶点在 所在直线的上方作 .
(1)当 经过点 时,
①请直接填空: (可能,不可能)过 点;(图1仅供分析)
②如图2,在 上截取 ,过 点作 垂直于直线 ,垂足为点 ,作 于 ,求证:四边形 为正方形.
(2)当 不过点 时,设 交边 于 ,且 .在 上存在点 ,过 点作 垂直于直线 ,垂足为点 ,使得 ,连接 ,求四边形 的最大面积.
今年四月份,某校在孝感市争创“全国文明城市”活动中,组织全体学生参加了“弘扬孝德文化,争做文明学生”的知识竞赛,赛后随机抽取了部分参赛学生的成绩,按得分划分成 , , , , , 六个等级,并绘制成如下两幅不完整的统计图表.
|
等级 |
得分 (分 |
频数(人 |
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
24 |
|
|
|
8 |
|
|
|
4 |
请根据图表提供的信息,解答下列问题:
(1)本次抽样调查样本容量为 ,表中: , ;扇形统计图中, 等级对应扇形的圆心角 等于 度;
(2)该校决定从本次抽取的 等级学生(记为甲、乙、丙、丁)中,随机选择2名成为学校文明宣讲志愿者,请你用列表法或画树状图的方法,求恰好抽到甲和乙的概率.