小明在解决问题：已知a=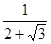
,求
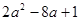的值．
他是这样分析与解的：∵a==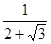
，
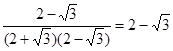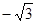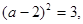
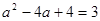
∴a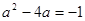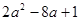-2=
,∴
∴
,∴=2（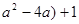
=2×（-1）+1=-1．
请你根据小明的分析过程，解决如下问题：
（1）化简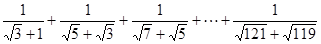
（2）若a=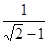
,①求
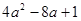的值；
②直接写出代数式的值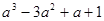
= ；
= ．
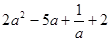一家用电器开发公司研制出一种新型的电子产品，每件的生产成本为18元，按定价40元出售，每月可销售20万件．为了增加销售量，公司决定采取降价的办法，经市场调研，每降价1元，月销售量可增加2万件．
（1）求出月销售量y（万件）与销售单价x（元）之间的函数关系式（不必写出x的取值范围）；
（2）求出月销售利润z（万元）（利润＝售价－成本价）与销售单价x（元）之间的函数关系式（不必写出x的取值范围）．
（3）若某月利润为350万元时，则该月销售量为多少万件，此时销售单价为多少元？
如图所示，在
△
中，
，
，将
绕点
沿逆时针方向旋转
得到
．
（1）线段
的长是 ，
的度数是 ；
（2）连接
，求证：四边形
是平行四边形．
如图，王强在一次高尔夫球的练习中，在某处击球，其飞行路线满足抛物线
，其中y（m）是球的飞行高度，x（m）是球飞出的水平距离，结果球离球洞的水平距离还有2m．
（1）请写出抛物线的开口方向、顶点坐标、对称轴．
（2）请求出球飞行的最大水平距离．
（3）若王强再一次从此处击球，要想让球飞行的最大高度不变且球刚好进洞，则球飞行路线应满足怎样
的抛物线，求出其解析式
阅读材料：设一元二次方程ax2+bx+c＝0（a≠0）的两根为x1，x2，则两根与方程系数之间有如下关系：x1+x2＝－
，x1·x2＝
．请根据该材料解题：已知x1，x2是方程x2+6x+3＝0的两实数根，求
和
的值．
如图，方格纸中的每个都是边长为1的正方形，将△OAB绕点O按顺时针方向旋转90°得到△OA′B′．
（1）在给定的方格纸中画出△OA′B′；
（2）求出OA，AA′的长为．