如图口袋中有5张完全相同的卡片,分别写有1 cm、2 cm、3 cm、4 cm、5 cm,口袋外有2张卡片,分别写有4 cm和5 cm ,现随机从袋内取出一张卡片,与口袋外两张卡片放在一起,以卡片上的数字分别作为三条线段的长度,回答下列问题: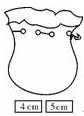
(1)求这三条线段能构成三角形的概率;
(2)求这三条线段能构成直角三角形的概率.
在平面直角坐标中,直角三角板
 ,将直角顶点
,将直角顶点 放在点(
放在点( ,1)处,
,1)处, ∥
∥ ,求经过点C的反比例函数的解析式.
,求经过点C的反比例函数的解析式.
如图①,在平面直角坐标系中,已知△ABC是等边三角形,点B的坐标为(12,0),动点P在线段AB上从点A向点B以每秒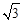 个单位的速度运动,设运动时间为t秒.以点P为顶点,作等边△PMN,点M,N在x轴上.
个单位的速度运动,设运动时间为t秒.以点P为顶点,作等边△PMN,点M,N在x轴上.
当t为何值时,点M与点O重合.
求点P坐标和等边△PMN的边长(用t的代数式表示).
如果取OB的中点D,以OD为边在△AOB内部作如图②所示的矩形ODEF,点E在线段AB上.设等边△PMN和矩形ODEF重叠部分的面积为S,请求出当
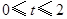 秒时S与
秒时S与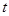 的函数关系式,并求出S的最大值.
的函数关系式,并求出S的最大值.
两个全等的直角三角形ABC和DEF重叠在一起,其中∠A=60°,AC=1.固定△ABC不动,将△DEF进行如下操作:如图1,△DEF沿线段AB向右平移(即D点在线段AB内移动),连结DC、CF、FB,四边形CDBF的形状在不断的变化,但它的面积不变化,四边形CDBF面积为▲;
如图2,当D点移到AB的中点时,请你猜想四边形CDBF的形状,并说明理由.
如图3,△DEF的D点固定在AB的中点,然后绕D点按顺时针方向旋转△DEF,使DF落在AB边上,此时F点恰好与B点重合,连结AE,请你求出sin∠AED的值.


某市种植某种绿色蔬菜,全部用来出口.为了扩大出口规模,该市决定对这种蔬菜的种植实行政府补贴,规定每种植一亩这种蔬菜一次性补贴菜农若干元.经调查,种植亩数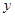 (亩)与补贴数额
(亩)与补贴数额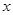 (元)之间大致满足如图1所示的一次函数关系.随着补贴数额
(元)之间大致满足如图1所示的一次函数关系.随着补贴数额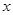 的不断增大,出口量也不断增加,但每亩蔬菜的收益
的不断增大,出口量也不断增加,但每亩蔬菜的收益 (元)会相应降低,且
(元)会相应降低,且 与
与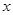 之间也大致满足如图2所示的一次函数关系.
之间也大致满足如图2所示的一次函数关系.在政府未出台补贴措施前,该市种植这种蔬菜的总收益额为多少?
求政府补贴政策实施后,种植亩数
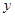 、每亩蔬菜的收益
、每亩蔬菜的收益 分别与政府补贴数额
分别与政府补贴数额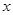 之间的函数关系式;
之间的函数关系式;要使全市种植这种蔬菜的总收益
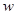 (元)最大,政府应将每亩补贴数额
(元)最大,政府应将每亩补贴数额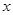 定为多少?并求出总收益
定为多少?并求出总收益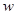 的最大值.
的最大值.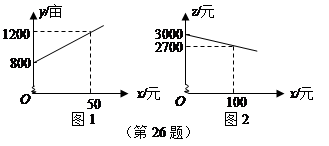
如图,AB是半圆O上的直径,E是的中点,OE交弦BC于点D,过点C作⊙O切线交OE的延长线于点F. 已知BC=8,DE=2.求⊙O的半径;
求CF的长;
求tan∠BAD 的值
