(1)已知:如图1,在Rt△ABC中,∠C=90°,BC=4,tanB= .求sinA的值.
.求sinA的值.
(2)已知:如图2,点E是正方形ABCD内一点,△CDE是等边三角形,连接EB、EA.求证:△ADE≌△BCE;
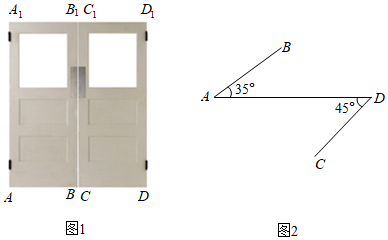
如图1是某中学教学楼的推拉门,已知门的宽度 米,且两扇门的大小相同(即 ,将左边的门 绕门轴 向里面旋转 ,将右边的门 绕门轴 向外面旋转 ,其示意图如图2,求此时 与 之间的距离(结果保留一位小数).(参考数据: , ,
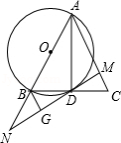
如图,在 中, 是 边上的中线,以 为直径的 交 于点 ,过 作 于点 ,交 的延长线于点 ,过点 作 于 .
(1)求证: ;
(2)求证:直线 是 的切线.
如图, 是 的对角线.
(1)尺规作图(请用 铅笔):作线段 的垂直平分线 ,交 , , 分别于 , , ,连接 , (保留作图痕迹,不写作法).
(2)试判断四边形 的形状并说明理由.

先化简,再求值: ,其中 .
如图,在平面直角坐标系中,抛物线 经过坐标原点,与 轴正半轴交于点 ,点 是抛物线上一动点.
(1)如图1,当 , ,且 时,
①求点 的坐标;
②若点 , 在该抛物线上,连接 , , 是线段 上一动点(点 与点 , 不重合),过点 作 ,交 轴于点 ,线段 与 是否相等?请说明理由;
(2)如图2,该抛物线的对称轴交 轴于点 ,点 在对称轴上,当 , ,且直线 交 轴的负半轴于点 时,过点 作 轴的垂线,交直线 于点 , 为 轴上一点,点 的坐标为 ,连接 .若 ,求证:射线 平分 .
