(本小题满分13分,(1)小问7分,(2)小问6分)
已知函数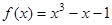 ,
,
(1)求函数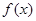 在点
在点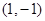 处的切线方程;
处的切线方程;
(2)求函数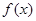 的单调递减区间.
的单调递减区间.
在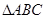 中,角
中,角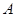 、
、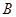 、
、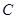 所对的边分别是
所对的边分别是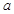 、
、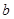 、
、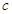 , 向量
, 向量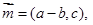
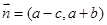 ,且
,且 与
与 共线.
共线.
(1)求角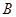 的大小;
的大小;
(2)设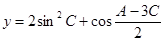 ,求
,求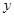 的最大值及此时角
的最大值及此时角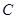 的大小.
的大小.
在△ABC中,角A,B,C所对的边分别为a,b,c, cosC+(cosA-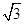 sinA)cosB=0.
sinA)cosB=0.
(1)求角B的大小;
(2)若a+c=1,求b的取值范围
已知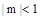 ,直线
,直线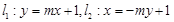 ,
,  相交于点P,
相交于点P, 交y轴于点A,
交y轴于点A, 交x轴于点B
交x轴于点B
(1)证明: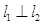 ;
;
(2)用m表示四边形OAPB的面积S,并求出S的最大值;
(3)设S=" f" (m), 求 的单调区间.
的单调区间.
若 且 .
(I)求
的最小值;
(II)是否存在
,使得
?并说明理由.
已知曲线
,直线
(t为参数)
(1)写出曲线
的参数方程,直线
的普通方程;
(2)过曲线 上任意一点 作与 夹角为30°的直线,交 于点A,求 的最大值与最小值.