已知椭圆: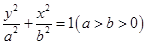 ,离心率为
,离心率为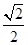 ,焦点
,焦点 过
过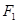 的直线交椭圆于
的直线交椭圆于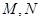 两点,且
两点,且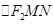 的周长为4.
的周长为4.
(Ⅰ)求椭圆方程;
(Ⅱ) 直线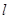 与y轴交于点P(0,m)(m
与y轴交于点P(0,m)(m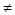 0),与椭圆C交于相异两点A,B且
0),与椭圆C交于相异两点A,B且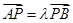 .若
.若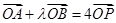 ,求m的取值范围。
,求m的取值范围。
双曲线的离心率等于2,且与椭圆 有相同的焦点,求此双曲线方程.
有相同的焦点,求此双曲线方程.
为了绿化城市,准备在如图所示的区域内修建一个矩形PQRC的草坪,且PQ∥BC,RQ⊥BC,另外△AEF的内部有一文物保护区不能占用,经测量AB=100m,BC=80m,AE=30m,AF=20m.
(1)求直线EF的方程(4 分 ).
(2)应如何设计才能使草坪的占地面积最大?
一圆与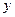 轴相切,圆心在直线
轴相切,圆心在直线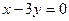 上,在
上,在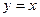 上截得的弦长为
上截得的弦长为 ,求此圆的方程.
,求此圆的方程.
已知三角形ABC的顶点坐标为A(-1,5)、B(-2,-1)、C(4,3),M是BC边上的中点.
(Ⅰ)求AB边所在的直线方程;
(Ⅱ)求中线AM的长.
已知圆台的上、下底面半径分别是2、6,且侧面面积等于两底面面积之和.
(Ⅰ)求该圆台的母线长;
(Ⅱ)求该圆台的体积.