为了绿化城市,准备在如图所示的区域内修建一个矩形PQRC的草坪,且PQ∥BC,RQ⊥BC,另外△AEF的内部有一文物保护区不能占用,经测量AB=100m,BC=80m,AE=30m,AF=20m.
(1) 求直线EF的方程(4 分 ).
(2) 应如何设计才能使草坪的占地面积最大?
(本小题满分14分)下面的茎叶图记录了甲、乙两代表队各10名同学在一次英语听力比赛中的成绩(单位:分).已知甲代表队数据的中位数为76,乙代表队数据的平均数是75.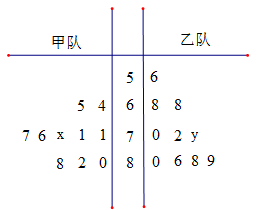
(1)求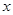 ,
,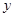 的值;
的值;
(2)若分别从甲、乙两队随机各抽取1名成绩不低于80分的学生,求抽到的学生中,甲队学生成绩不低于乙队学生成绩的概率;
(3)判断甲、乙两队谁的成绩更稳定,并说明理由(方差较小者稳定).
在平面直角坐标系上,第二象限角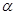 的终边与单位圆交于点
的终边与单位圆交于点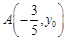 .
.
(1)求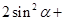
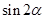 的值;
的值;
(2)若向量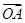 与
与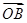 夹角为
夹角为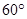 ,且
,且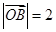 ,求直线
,求直线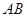 的斜率.
的斜率.
(本小题满分14分)已知数列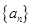 的前
的前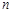 项和
项和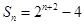 .
.
(1)求数列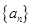 的通项公式;
的通项公式;
(2)设等差数列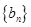 满足
满足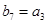 ,
,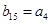 ,求数列
,求数列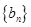 的前
的前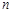 项和
项和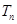 .
.
(本小题满分12分)已知向量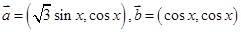 ,函数
,函数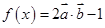
(1)求 的对称轴。
的对称轴。
(2)当 时,求
时,求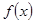 的最大值及对应的
的最大值及对应的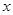 值。
值。
(本小题满分12分)已知向量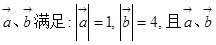 的夹角为
的夹角为 .
.
(1)求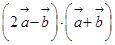 ;(2)若
;(2)若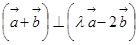 ,求
,求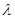 的值.
的值.