(1)如图1,△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE.①∠AEB的度数为 ;② 线段AD,BE之间的数量关系为 ;
(2)如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A,D,E在同一直线上,CM为△DCE中DE边上的高,连接BE,请判断∠AEB的度数及线段CM,AE,BE之间的数量关系,并说明理由;
(3)如图3,在正方形ABCD中,CD=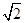 ,若点P满足PD=1,且∠BPD=90°,请直接写出点A到BP的距离.
,若点P满足PD=1,且∠BPD=90°,请直接写出点A到BP的距离.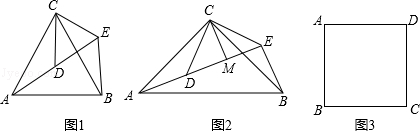
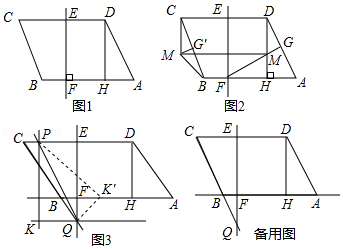
如图1,在 中, 于点 , 的垂直平分线交 于点 ,交 于点 , , , .
(1)如图2,作 于点 ,交 于点 ,将 沿 方向平移,得到△ ,连接 .
①求四边形 的面积;
②直线 上有一动点 ,求 周长的最小值.
(2)如图3,延长 交 于点 ,过点 作 ,过 边上的动点 作 ,并与 交于点 ,将 沿直线 翻折,使点 的对应点 恰好落在直线 上,求线段 的长.
为落实“绿水青山就是金山银山”的发展理念,某市政部门招标一工程队负责在山脚下修建一座水库的土方施工任务.该工程队有 , 两种型号的挖掘机,已知3台 型和5台 型挖掘机同时施工一小时挖土165立方米;4台 型和7台 型挖掘机同时施工一小时挖土225立方米.每台 型挖掘机一小时的施工费用为300元,每台 型挖掘机一小时的施工费用为180元.
(1)分别求每台 型, 型挖掘机一小时挖土多少立方米?
(2)若不同数量的 型和 型挖掘机共12台同时施工4小时,至少完成1080立方米的挖土量,且总费用不超过12960元,问施工时有哪几种调配方案,并指出哪种调配方案的施工费用最低,最低费用是多少元?
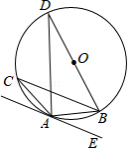
如图, 为 外接圆 的直径,且 .
(1)求证: 与 相切于点 ;
(2)若 , , ,求 的长.
为进一步提高全民“节约用水”意识,某学校组织学生进行家庭月用水量情况调查活动,小莹随机抽查了所住小区 户家庭的月用水量,绘制了下面不完整的统计图.
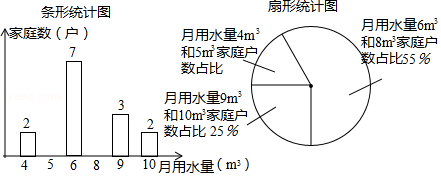
(1)求 并补全条形统计图;
(2)求这 户家庭的月平均用水量;并估计小莹所住小区420户家庭中月用水量低于月平均用水量的家庭户数;
(3)从月用水量为 和 的家庭中任选两户进行用水情况问卷调查,求选出的两户中月用水量为 和 恰好各有一户家庭的概率.
如图,点 是正方形 边 上一点,连接 ,作 于点 , 于点 ,连接 .
(1)求证: ;
(2)已知 ,四边形 的面积为24,求 的正弦值.
