(本小题满分12分)如图,平面直角坐标系中,抛物线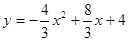 交
交 轴于A、B两点(点B在点A的右侧),交
轴于A、B两点(点B在点A的右侧),交 轴于点C,以OC、OB为两边作矩形OBDC,CD交抛物线于G.
轴于点C,以OC、OB为两边作矩形OBDC,CD交抛物线于G.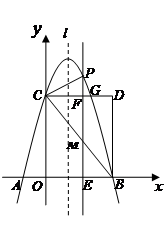
(1)求OC和OB的长;
(2)抛物线的对称轴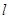 在边OB(不包括O、B两点)上作平行移动,交
在边OB(不包括O、B两点)上作平行移动,交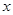 轴于点E,交CD于点F,交BC于点M,交抛物线于点P.设OE=m,PM=h,求h与m的函数关系式,并求出PM的最大值;
轴于点E,交CD于点F,交BC于点M,交抛物线于点P.设OE=m,PM=h,求h与m的函数关系式,并求出PM的最大值;
(3)在(2)的情况下,连接PC,则在CD上方的抛物线部分是否存在这样的点P,使得以P、C、F为顶点的三角形和△BEM相似?若存在,直接写出此时m的值,并直接判断此时△PCM的形状;若不存在,请说明理由.
如图1,矩形MNPQ中,点E,F,G,H分别在NP,PQ,QM,MN上,若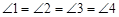 ,则称四边形EFGH为矩形MNPQ的反射四边形.图2,图3,图4中,四边形ABCD为矩形,且
,则称四边形EFGH为矩形MNPQ的反射四边形.图2,图3,图4中,四边形ABCD为矩形,且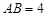 ,
,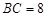 .
.
理解与作图:
(1)在图2,图3中,点E,F分别在BC,CD边上,试利用正方形网格在图上作出矩形ABCD的反射四边形EFGH.
计算与猜想:
(2)求图2,图3中反射四边形EFGH的周长,并猜想矩形ABCD的反射四边形的周长是否为定值?
启发与证明:
(3)如图4,为了证明上述猜想,小华同学尝试延长GF交BC的延长线于M,试利用小华同学给我们的启发证明(2)中的猜想.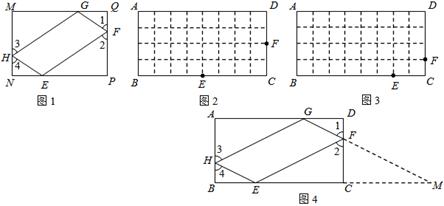
一辆快车从甲地驶往乙地,一辆慢车从乙地驶往甲地,两车同时出发,匀速行驶.设行驶的时间为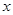 (时),两车之间的距离为
(时),两车之间的距离为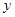 (千米),图中的折线表示从两车出发至快车到达乙地过程中
(千米),图中的折线表示从两车出发至快车到达乙地过程中 与
与 之间的函数关系.
之间的函数关系.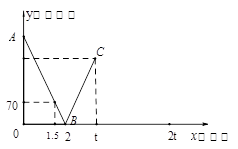
(1)根据图中信息,求线段AB所在直线的函数解析式和甲乙两地之间的距离;
(2)已知两车相遇时快车比慢车多行驶40千米,若快车从甲地到达乙地所需时间为t时,求t的值;
(3)若快车到达乙地后立刻返回甲地,慢车到达甲地后停止行驶,请你在图中画出快车从乙地返回到甲地过程中 关于
关于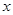 的函数的大致图象.
的函数的大致图象.
已知:用2辆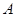 型车和1辆
型车和1辆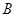 型车装满货物一次可运货10吨;用1辆
型车装满货物一次可运货10吨;用1辆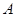 型车和2辆
型车和2辆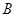 型车装满货物一次可运货11吨,某物流公司现有31吨货物,计划同时租用
型车装满货物一次可运货11吨,某物流公司现有31吨货物,计划同时租用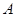 型车
型车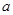 辆,
辆,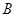 型车
型车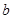 辆,一次运完,且恰好每辆车都装满货物.根据以上信息,解答下列问题:
辆,一次运完,且恰好每辆车都装满货物.根据以上信息,解答下列问题:
(1)1辆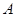 型车和1辆
型车和1辆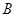 型车都装满货物一次可分别运货多少吨?
型车都装满货物一次可分别运货多少吨?
(2)请你帮该物流公司设计租车方案;
(3)若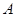 型车每辆需租金100元/次,
型车每辆需租金100元/次,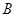 型车每辆需租金120元/次.请选出最省钱的租车方案,并求出最少租车费.
型车每辆需租金120元/次.请选出最省钱的租车方案,并求出最少租车费.
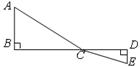
如图,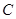 为线段
为线段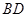 上一动点,分别过点
上一动点,分别过点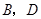 作
作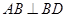 ,
,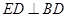 ,连接
,连接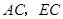 .已知
.已知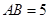 ,
,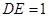 ,
,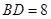 ,设
,设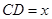 .
.
(1)用含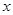 的代数式表示
的代数式表示 的长;
的长;
(2)请问点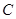 满足什么条件时,
满足什么条件时, 的值最小?
的值最小?
(3)根据(2)中的规律和结论,请构图求出代数式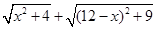 的最小值.
的最小值.
如图,已知菱形ABCD,AB=AC,E、F分别是BC、AD的中点,连接AE、CF.
(1)四边形AECF是什么特殊的四边形?说明理由;
(2)若AB=8,求菱形的面积.