甲、乙两个同学在直跑道上进行4×100 m接力(如图所示),他们在奔跑时有相同的最大速度,乙从静止开始全力奔跑需跑出25 m才能达到最大速度,这一过程可看作匀加速直线运动.现在甲持棒以最大速度向乙奔来,乙在接力区伺机全力奔出.若要求乙接棒时奔跑的速度达到最大速度的80%,则: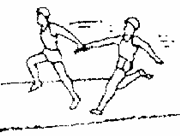
(1)乙在接力区须奔出多少距离?
(2)乙应在距离甲多远时起跑?
在研究摩擦力特点的实验中,将木块放在足够长的静止水平木板上。如图甲所示,用力沿水平方向拉木块,使拉力F从O开始逐渐增大.经实验绘制出摩擦力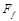 随拉力F的变化图像如图丙所示.已知木块质量为0.78 kg。
随拉力F的变化图像如图丙所示.已知木块质量为0.78 kg。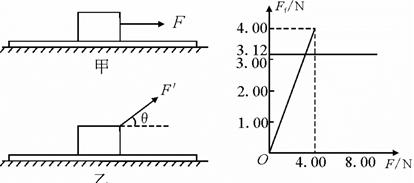
(1)求木块与长木板间的动摩擦因数。
(2)若木块在与水平方向成θ=37°角斜向右上方的恒定拉力F′作用下,以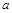 =2.0m/
=2.0m/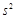 的加速度从静止开始做匀加速直线运动,如图乙所示,则F′为多大?(取sin 37°=0.6,COS 37°=0.8)
的加速度从静止开始做匀加速直线运动,如图乙所示,则F′为多大?(取sin 37°=0.6,COS 37°=0.8)
如图所示,为一传送货物的传送带abc,传送带的ab部分与水平面夹角 =37°,bc部分与水平面夹角
=37°,bc部分与水平面夹角 =53°,ab部分长为4.7m,bc部分长为7.5m。一个质量为m=1kg的物体A(可视为质点)与传送带的动摩擦因数
=53°,ab部分长为4.7m,bc部分长为7.5m。一个质量为m=1kg的物体A(可视为质点)与传送带的动摩擦因数 =0.8。传送带沿顺时针方向以速率ν=1m/s匀速转动.若把物体A轻放到a处,它将被传送带送到c处,此过程中物体A不会脱离传送带。(sin 37°=0.6,sin 53°=0.8,g=10m/
=0.8。传送带沿顺时针方向以速率ν=1m/s匀速转动.若把物体A轻放到a处,它将被传送带送到c处,此过程中物体A不会脱离传送带。(sin 37°=0.6,sin 53°=0.8,g=10m/ )求物体A从a处被传送到c处所用的时间。
)求物体A从a处被传送到c处所用的时间。
图中MN和PQ为竖直方向的两平行长直金属导轨,间距l为0.40m,电阻不计。导轨所在平面与磁感应强度B为0.50T的匀强磁场垂直。质量m为6.0×10-3kg.电阻为1.0 的金属杆ab始终垂直于导轨,并与其保持光滑接触。导轨两端分别接有滑动变阻器和阻值为3.0
的金属杆ab始终垂直于导轨,并与其保持光滑接触。导轨两端分别接有滑动变阻器和阻值为3.0 的电阻R1。当杆ab达到稳定状态时以速率v匀速下滑,整个电路消耗的电功率P为0.27W,重力加速度取10m/s2,试求速率v和滑动变阻器接入电路部分的阻值R2。
的电阻R1。当杆ab达到稳定状态时以速率v匀速下滑,整个电路消耗的电功率P为0.27W,重力加速度取10m/s2,试求速率v和滑动变阻器接入电路部分的阻值R2。
如图所示,两足够长的光滑金属导轨竖直放置,相距为L,一理想电流表与两导轨相连,匀强磁场与导轨平面垂直。一质量为m.有效电阻为R的导体棒在距磁场上边界h处静止释放。导体棒进入磁场后,流经电流表的电流逐渐减小,最终稳定为I。整个运动过程中,导体棒与导轨接触良好,且始终保持水平,不计导轨的电阻。求:
(1)磁感应强度的大小B;
(2)电流稳定后,导体棒运动速度的大小 ;
;
(3)流经电流表电流的最大值 。
。
如图甲所示,在水平面上固定有长为L=2m.宽为d=1m的金属“U”形导轨,在“U”形导轨右侧 =0.5m范围内存在垂直纸面向里的匀强磁场,且磁感应强度随时间变化规律如图乙所示。在t=0时刻,质量为m=0.1kg的导体棒以v0=lm/s的初速度从导轨的左端开始向右运动,导体棒与导轨之间的动摩擦因数为μ=0.1,导轨与导体棒单位长度的电阻均为λ=0.1
=0.5m范围内存在垂直纸面向里的匀强磁场,且磁感应强度随时间变化规律如图乙所示。在t=0时刻,质量为m=0.1kg的导体棒以v0=lm/s的初速度从导轨的左端开始向右运动,导体棒与导轨之间的动摩擦因数为μ=0.1,导轨与导体棒单位长度的电阻均为λ=0.1 /m,不计导体棒与导轨之间的接触电阻及地球磁场的影响(取g="10" m/s2)。
/m,不计导体棒与导轨之间的接触电阻及地球磁场的影响(取g="10" m/s2)。
(1)通过计算分析4s内导体棒的运动情况;
(2)计算4s内回路中电流的大小,并判断电流方向;
(3)计算4s内回路产生的焦耳热。