如图1,小明将量角器和一块含30°角的直角三角板ABC紧靠着放在同一平面内,使直角边BC与量角器的0°线CD在同一直线上(即点B、C、O、D在同一直线上),O为量角器圆弧所在圆的圆心,∠ACB=90°,∠CAB=30°,BC=6cm.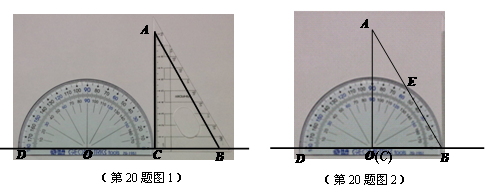
(1)判断AC是不是⊙O的切线,并说明理由.
(2)将直角三角板ABC沿CD方向平移,使点C落在点O上.此时点B落在点C原位置上(如图2),AB交⊙O于点E,则弧BE的长是多少?
(本题12分)已知两直线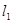 ,
,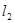 分别经过点A(3,0),点B(-1,0),并且当两直线同时相交于y负半轴的点C时,恰好有
分别经过点A(3,0),点B(-1,0),并且当两直线同时相交于y负半轴的点C时,恰好有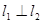 ,经过点A、B、C的抛物线的对称轴与直线
,经过点A、B、C的抛物线的对称轴与直线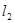 交于点D,如图所示。
交于点D,如图所示。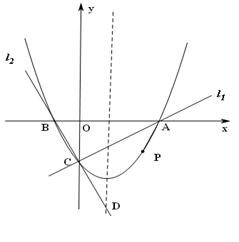
(1)求抛物线的函数解析式;
(2)当直线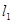 绕点C顺时针旋转一个锐角时,它与抛物线的另一个交点为P(x,y),求四边形APCB面积S关于x的函数解析式,并求S的最大值;
绕点C顺时针旋转一个锐角时,它与抛物线的另一个交点为P(x,y),求四边形APCB面积S关于x的函数解析式,并求S的最大值;
(3)当直线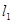 绕点C旋转时,它与抛物线的另一个交点为P,请找出使△PCD为等腰三角形的点P,并求出点P的坐标。
绕点C旋转时,它与抛物线的另一个交点为P,请找出使△PCD为等腰三角形的点P,并求出点P的坐标。
(本题10分)如图,点E是矩形ABCD中CD边上一点,△BCE沿BE折叠为△BFE,点F落在AD上。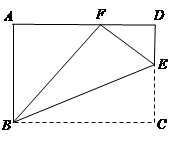
(1)求证:△ABF∽△DFE;
(2)若△BEF∽△ABF,求CD∶BC的值。
(本题10分)在直角坐标系中,有如图所示的Rt△ABO,AB⊥x轴于点B(8,0),斜边AO=10,C为AO的中点,反比例函数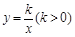 的图象经过点C,且与AB交于点D。
的图象经过点C,且与AB交于点D。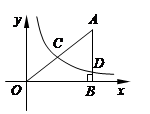
(1)求此反比例函数的解析式;
(2)求线段AD的长度。
(本题10分)如图,在四边形ABCD中,AB=2,CD=1,∠A=61°,
∠ADC=∠B=90°,利用解直角三角形知识求这个四边形ABCD的面积。
(结果精确到0.1。下列数据供参考: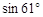 ≈0.87,
≈0.87,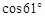 ≈0.48,
≈0.48,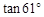 ≈1.80;
≈1.80;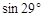 ≈0.48,
≈0.48,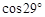 ≈0.87,
≈0.87,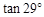 ≈0.55)
≈0.55)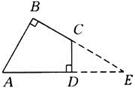
(本题8分)如图,已知在⊙O中,∠ABD=∠CDB。
(1)求证:AB=CD;
(2)顺次连结ACBD四点,猜想得到的是哪种特殊的四边形?并说明理由。