定义:有一组对角相等而另一组对角不相等的凸四边形叫做“等对角四边形”.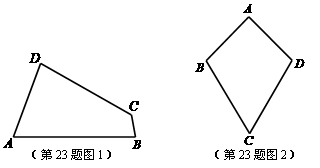
(1)已知:如图1,四边形 是“等对角四边形”,
是“等对角四边形”,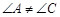 ,
,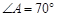 ,
,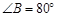 .求
.求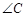 ,
,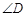 的度数.
的度数.
(2)在探究“等对角四边形”性质时:
① 小红画了一个“等对角四边形” (如图2),其中
(如图2),其中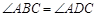 ,
,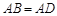 ,此时她发现
,此时她发现 成立.请你证明此结论.
成立.请你证明此结论.
② 由此小红猜想:“对于任意‘等对角四边形’,当一组邻边相等时,另一组邻边也相等”.你认为她的猜想正确吗?若正确,请证明;若不正确,请举出反例.
(3)已知:在“等对角四边形” 中,
中,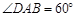 ,
,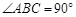 ,
,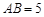 ,
,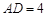 .求对角线
.求对角线 的长.
的长.
某生姜种植基地计划种植A、B两种生姜30亩.已知A、B两种生姜的年产量分别为2000千克/亩、2500千克/亩,收购单价分别是8元/千克、7元/千克.(1)若该基地全年收获A、B两种生姜的年总产量为68000千克,求A、B两种生姜各种多少亩?
(2)若要求种植A种生姜的亩数不少于B种的一半,那么种植A、B两种生姜各多少亩时,全部收购该基地生姜的年总收入最多?最多是多少元?
如图,在△ABC中,点E是AC边上的中点,点F是AB边上的中点,连结EF并延长至点D,再连结BD,请你添加一个条件,使BD=CE(不再添加其它线段,不再标注或使用其他字母), 并给出证明,添加的条件是: ▲.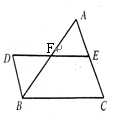
(1)计算:
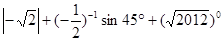 ;
;(2)先化简,再求值:
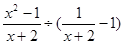 ,其中
,其中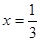 ·
·
如图,在平面直角坐标系中,直角梯形 的边
的边 落在
落在 轴的正半轴上,且
轴的正半轴上,且 ∥
∥ ,
, ,
, =4,
=4, =6,
=6, =8.正方形
=8.正方形 的两边分别落在坐标轴上,且它的面积等于直角梯形
的两边分别落在坐标轴上,且它的面积等于直角梯形 面积。将正方形
面积。将正方形 沿
沿 轴的正半轴平行移动,设它与直角梯形
轴的正半轴平行移动,设它与直角梯形 的重叠部分面积为
的重叠部分面积为 。
。(1)分析与计算:
求正方形 的边长;
的边长;(2)操作与求解:
①正方形 平行移动过程中,通过操作、观察,试判断
平行移动过程中,通过操作、观察,试判断 (
( >0)的变化情况是;
>0)的变化情况是;
| A.逐渐增大 | B.逐渐减少 | C.先增大后减少 | D.先减少后增大 |
②当正方形 顶点
顶点 移动到点
移动到点 时,求
时,求 的值;
的值;(3)探究与归纳:
设正方形 的顶点
的顶点 向右移动的距离为
向右移动的距离为 ,求重叠部分面积
,求重叠部分面积 与
与 的函数关系式。
的函数关系式。
已知抛物线 与x轴交于两点
与x轴交于两点 、
、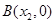
 ,与y轴交于点C,AB=6.
,与y轴交于点C,AB=6.(1)求抛物线和直线BC的解析式.
(2)在直角坐标系中,画出抛物线和直线BC.
(3)若⊙P过A、B、C三点,求⊙P的半径.
(4)抛物线上是否存在点M,过点M作
 轴于点N,使
轴于点N,使 被直线BC分成面积比为
被直线BC分成面积比为 的两部分?若存在,请求出点M的坐标;若不存在,请说明理由
的两部分?若存在,请求出点M的坐标;若不存在,请说明理由