(本小题满分14分)已知函数 .
.
(1)求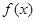 的单调递增区间;
的单调递增区间;
(2)若 是第二象限角,
是第二象限角,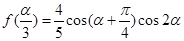 ,求
,求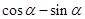 的值.
的值.
(本小题满分10分)
如图, 的直径
的直径 的延长线与弦
的延长线与弦 的延长线相交于点
的延长线相交于点 ,
, 为
为 上一点,
上一点, ,
, 交
交 于点
于点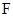 ,且
,且 .
.
(1)求 的长度;
的长度;
(2)若圆 与圆
与圆 内切,直线
内切,直线 与圆
与圆 切于点
切于点 ,求线段
,求线段 的长度.
的长度.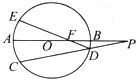
(本小题满分12分)
已知 ,
,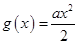 ,直线
,直线
 .
.
(1)函数 在
在 处的切线与直线
处的切线与直线 平行,求实数
平行,求实数 的值;
的值;
(2)若至少存在一个 使
使 成立,求实数
成立,求实数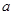 的取值范围;
的取值范围;
(3)设 ,当
,当 时
时 的图象恒在直线
的图象恒在直线 的上方,求
的上方,求 的最大值.
的最大值.
(本题小满分12分)
如图,直三棱柱 中,
中, ,
, 分别是
分别是 ,
, 的中点,
的中点, .
.
(1)证明: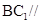 平面
平面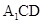 ;
;
(2)求异面直线 和
和 所成角的大小;
所成角的大小;
(3)当 时,求三棱锥
时,求三棱锥 的体积.
的体积.
(本小题满分12分)
已知等比数列 的公比
的公比 ,
, 且
且 ,
, ,
, 成等差数列.数列
成等差数列.数列 的前
的前 项和为
项和为 ,且
,且 .
.
(1)分别求出数列 和数列
和数列 的通项公式;
的通项公式;
(2)设 ,若
,若 ,对于
,对于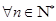 恒成立,求实数
恒成立,求实数 的最小值.
的最小值.
如图,四棱锥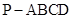 ,侧面
,侧面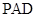 是边长为
是边长为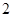 的正三角形,且与底面垂直,底面
的正三角形,且与底面垂直,底面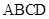 是
是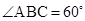 的菱形,
的菱形,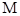 为
为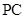 的中点.
的中点.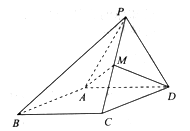
(1)求证: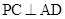 ;
;
(2)求点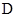 到平面
到平面 的距离.
的距离.