抛物线M: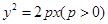 的准线过椭圆N:
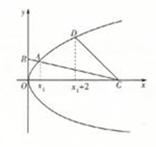
的准线过椭圆N: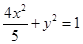 的左焦点,以坐标原点为圆心,以t(t>0)为半径的圆分别与抛物线M在第一象限的部分以及y轴的正半轴相交于点A与点B,直线AB与x轴相交于点C.
的左焦点,以坐标原点为圆心,以t(t>0)为半径的圆分别与抛物线M在第一象限的部分以及y轴的正半轴相交于点A与点B,直线AB与x轴相交于点C.
(1)求抛物线M的方程.
(2)设点A的横坐标为x1,点C的横坐标为x2,曲线M上点D的横坐标为x1+2,求直线CD的斜率.
(本小题满分10分)已知数列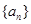 各项均为正,且
各项均为正,且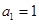 ,
,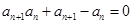
 .
.
(1)设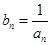 ,求证:数列
,求证:数列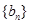 是等差数列;
是等差数列;
(2)求数列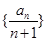 的前n项和
的前n项和 .
.
(本小题满分12分)设 ,
,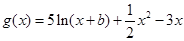 ,函数
,函数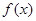 在
在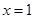 与
与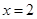 处取得极值.
处取得极值.
(1)求实数a,b的值;
(2)若 ,求证:当
,求证:当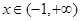 时,
时,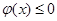 恒成立;
恒成立;
(3)证明:若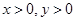 ,则
,则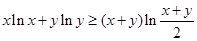 .
.
(本小题满分12分)已知点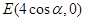 ,
,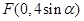
 为平面直角坐标系
为平面直角坐标系 中的点,点P为线段EF的中点,当
中的点,点P为线段EF的中点,当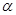 变化时,点P形成的轨迹
变化时,点P形成的轨迹 与x轴交于点A,B(A点在左侧),与y轴正半轴交于点C.
与x轴交于点A,B(A点在左侧),与y轴正半轴交于点C.
(1)求P点的轨迹 的方程;
的方程;
(2)设点M是轨迹 上任意一点(不在坐标轴上),直线CM交x轴于点D,直线BM交直线AC于点N.
上任意一点(不在坐标轴上),直线CM交x轴于点D,直线BM交直线AC于点N.
①若D点坐标为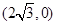 ,求线段CM的长;
,求线段CM的长;
②求证: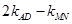 为定值.
为定值.
(本小题满分12分)在如图所示的几何体中, 与
与 都是边长为2的等比三角形且所在平面互相平行,四边形BCED为正方形,
都是边长为2的等比三角形且所在平面互相平行,四边形BCED为正方形, ,O,G分别是BC,DE的中点.
,O,G分别是BC,DE的中点.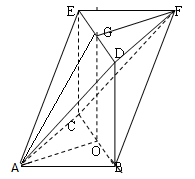
(1)证明:平面ADE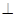 平面AOFG;
平面AOFG;
(2)求二面角D-AE-F的余弦值.
(本小题满分12分)已知在数列 中,
中,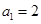 ,
, ,
,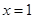 是函数
是函数 的一个极值点.
的一个极值点.
(1)证明:数列 为等比数列,并求数列
为等比数列,并求数列 的通项公式
的通项公式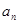 ;
;
(2)是否存在指数函数 ,使得对于任意的正整数n有
,使得对于任意的正整数n有 成立?若存在,求出满足条件的一个
成立?若存在,求出满足条件的一个 ;若不存在,请说明理由.
;若不存在,请说明理由.