(本小题满分12分)已知函数
(1)求函数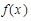 的最小正周期及在
的最小正周期及在 单调递增区间;
单调递增区间;
(2)在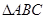 中,A、B、C分别为三边
中,A、B、C分别为三边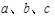 所对的角,若
所对的角,若 ,求
,求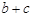 的最大值.
的最大值.
(本小题满分10分) 、
、 、
、 、
、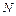 四点都在椭圆
四点都在椭圆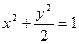 上,
上,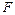 为椭圆在
为椭圆在 轴正半轴上的焦点,已
轴正半轴上的焦点,已 知
知 与
与 共线,
共线,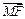 与
与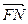 共线,且
共线,且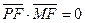 ,求四边形
,求四边形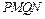 的面积的最小值和最大值。
的面积的最小值和最大值。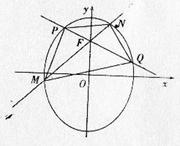
(本小题满分10分)
已知函数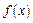 满足
满足
(1)求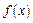 的解析式,并判断
的解析式,并判断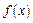 在
在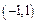 上的单调性(不须证明);
上的单调性(不须证明);
(2)对定义在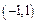 上的函数
上的函数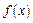 ,若
,若 ,求
,求 的取值范围;
的取值范围;
(3)当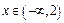 时,关于
时,关于 的不等式
的不等式 恒成立
恒成立 ,求
,求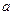 的取值范围.
的取值范围.
(本小题满分8分)已知函数
 ,其中
,其中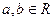 ,
,
(1)若曲线 在点
在点 处的切线方程为
处的切线方程为 ,求函数
,求函数 的解析式
的解析式
(2)讨论函数 的单调性
的单调性
(本小题满分6分)已知双曲线
(1)求双曲线的渐近线方程;
(2)试问过点 能否作直线
能否作直线 ,使
,使 与双曲线交于两点
与双曲线交于两点 ,且点A是线段
,且点A是线段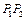 的中点?这样的直线存在吗?若存在,求出直线
的中点?这样的直线存在吗?若存在,求出直线 的方程,若不存在,说明理由。
的方程,若不存在,说明理由。
(本小题满分6分)已知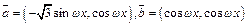 (
(
 ),函数
),函数 ,且
,且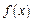 的最小正周期为
的最小正周期为 ,
,
(1)求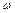 的值;
的值;
(2)求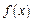 的单调区间.
的单调区间.