(本小题满分13分)已知椭圆C的中心在原点,焦点在x轴上,离心率等于 ,它的一个顶点恰好是抛物线
,它的一个顶点恰好是抛物线 的焦点.
的焦点.

(Ⅰ)求椭圆C的方程;
(Ⅱ)点P(2,3), Q(2,-3)在椭圆上,A,B是椭圆上位于直线PQ两恻的动点,
①若直线AB的斜率为 ,求四边形APBQ面积的最大值;
,求四边形APBQ面积的最大值;
②当A、B运动时,满足于∠APQ=∠BPQ,试问直线AB的斜率是否为定值,请说明理由.
一台机器使用的时间较长,但还可以使用,它按不同的转速生产出来的某机械零件有一些会有缺点,每小时生产有缺点零件的多少,随机器的运转的速度而变化,下表为抽样试验的结果:
转速x(转/秒) |
16 |
14 |
12 |
8 |
| 每小时生产有缺点的零件数y(件) |
11 |
9 |
8 |
5 |
画出散点图,并通过散点图确定变量y对x是否线性相关;
(2)如果y对x有线性相关关系,求回归直线方程;
(3)若实际生产中,允许每小时的产品中有缺点的零件最多为10个,那么机器的运转速度应控制在什么范围内?(精确到0.0001)
已知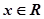 ,
, ,
,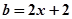 。求证
。求证 中至少有一个不少于0。
中至少有一个不少于0。
已知复数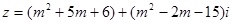 (
(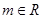 ),
),
试问m为何值时,(1) 为实数? (2)
为实数? (2) 所对应的点落在第三象限?
所对应的点落在第三象限?
已知集合 ,集合B=
,集合B=
(1)当 时,求
时,求 ;(2)若
;(2)若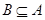 ,求
,求 的取值范围.
的取值范围.
已知函数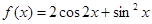
(1)求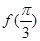 的值;(2)求
的值;(2)求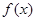 的最大值和最小值;
的最大值和最小值;
(3)求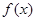 的单调递增区间.
的单调递增区间.