已知函数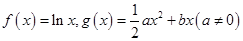 .
.
(Ⅰ)若 时,函数
时,函数 在其定义域上是增函数,求b的取值范围;
在其定义域上是增函数,求b的取值范围;
(Ⅱ)在(Ⅰ)的结论下,设函数 ,求函数
,求函数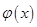 的最小值;
的最小值;
(Ⅲ)设函数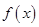 的图象
的图象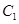 与函数
与函数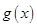 的图象
的图象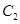 交于P、Q,过线段PQ的中点R作
交于P、Q,过线段PQ的中点R作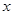 轴的垂线分别交
轴的垂线分别交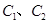 于点M、N,问是否存在点R,使
于点M、N,问是否存在点R,使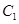 在M处的切线与
在M处的切线与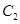 在N处的切线平行?若存在,求出R的横坐标;若不存在,请说明理由.
在N处的切线平行?若存在,求出R的横坐标;若不存在,请说明理由.
甲同学在军训中,练习射击项目,他射击命中目标的概率是 ,假设每次射击是否命中相互之间没有影响.
,假设每次射击是否命中相互之间没有影响.
(Ⅰ)在3次射击中,求甲至少有1次命中目标的概率;
(Ⅱ)在射击中,若甲命中目标,则停止射击,否则继续射击,直至命中目标,但射击次数最多不超过3次,求甲射击次数的分布列和数学期望.
在数列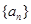 中,
中, ,
, ,
, 。
。
(Ⅰ)计算 ,
, ,
, 的值;
的值;
(Ⅱ)猜想数列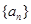 的通项公式,并用数学归纳法加以证明.
的通项公式,并用数学归纳法加以证明.
已知数列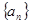 中,
中,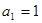 ,且
,且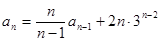 (
( )。
)。
(I)求 ,
, 的值及数列
的值及数列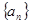 的通项公式;
的通项公式;
(II)(II)令 ,数列
,数列 的前
的前 项和为
项和为 ,试比较
,试比较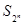 与
与 的大小;
的大小;
(III)令 ,数列
,数列 的前
的前 项和为
项和为 ,求证:对任意
,求证:对任意 ,都有
,都有 。
。
已知函数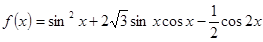 ,
,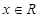 。
。
(I)求 的最小正周期和值域;
的最小正周期和值域;
(II)若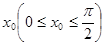 为
为 的一个零点,求
的一个零点,求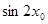 的值。
的值。
已知 为等比数列,
为等比数列, ,
,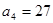 ,
,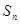 为等差数列
为等差数列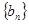 的前
的前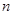 项和,
项和, ,
,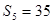 。
。
(I)求 和
和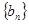 的通项公式;
的通项公式;
(II)设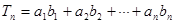 ,求
,求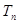 。
。