已知数列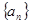 中,
中,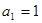 ,且
,且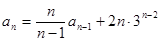 (
( )。
)。
(I) 求 ,
, 的值及数列
的值及数列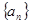 的通项公式;
的通项公式;
(II) (II)令 ,数列
,数列 的前
的前 项和为
项和为 ,试比较
,试比较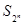 与
与 的大小;
的大小;
(III)令 ,数列
,数列 的前
的前 项和为
项和为 ,求证:对任意
,求证:对任意 ,都有
,都有 。
。
已知平面内一动点
到点
(1,0)的距离与点
到
轴的距离的等等于1.
(1)求动点
的轨迹 的方程;
的方程;
(2)过点
作两条斜率存在且互相垂直的直线
,设
与轨迹
相交于点
,
与轨迹
相交于点
,求
的最小值.
某企业在第
年初购买一台价值为
万元的设备
的价值在使用过程中逐年减少,从第
年到第
年,每年初
的价值比上年初减少
万元;从第
年开始,每年初
的价值为上年初的
.
(1)求第
年初
的价值
的表达式;
(2)设
,若
大于80万元,则
继续使用,否则须在第
年初对
更新,证明:须在第9年初对
更新.
如图,在圆锥
中,已知
,
的直径
,点
在
上,且
,
为
的中点.
(I)证明:
(II)求直线和平面 所成角的正弦值.
某河流上的一座水力发电站,每年六月份的发电量
(单位:万千瓦时)与该河上游在六月份的降雨量
(单位:毫米)有关.据统计,当
时,
;
每增加10,
增 加5;已知近20年
的值为:140,110,160,70,200,160,140,160,220,200,110,160,160,200,140,110,160,220,140,160.
加5;已知近20年
的值为:140,110,160,70,200,160,140,160,220,200,110,160,160,200,140,110,160,220,140,160.
(I)完成如下的频率分布表:
近20年六月份降雨量频率分布表
| 降雨量 |
70 |
 110 110 |
140 |
160 |
200 |
220 |
| 频率 |
(II)假定今年六月份的降雨量与近20年六月份的降雨量的分布规律相同,并将频率视为概率,求今 年六月份该水力发电站的发电量低于490(万千瓦时)或超过530(万千瓦时)的概率.
年六月份该水力发电站的发电量低于490(万千瓦时)或超过530(万千瓦时)的概率.
在 中,角 所对的边分别为 且满足 .
(I)求角
的大小;
(II)求
的最大值,并求取得最大值时角
的大小.