（理）在某校举行的数学竞赛中，全体参赛学生的竞赛成绩近似服从正态分布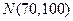
。已知成绩在90分以上（含90分）的学生有12名。
（Ⅰ）、试问此次参赛学生总数约为多少人？
（Ⅱ）、若该校计划奖励竞赛成绩排在前50名的学生，试问设奖的分数线约为多少分？可共查阅的（部分）标准正态分布表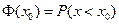
 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
| 1．2 1．3 1．4 1．9 2．0 2．1 |
0．8849 0．9032 0．9192 0．9713 0．9772 0．9821 |
0．8869 0．9049 0．9207 0．9719 0．9778 0．9826 |
0．888 0．9066 0．9222 0．9726 0．9783 0．9830 |
0．8907 0．9082 0．9236 0．9732 0．9788 0．9834 |
0．8925 0．9099 0．9251 0．9738 0．9793 0．9838 |
0．8944 0．9115 0．9265 0．9744 0．9798 0．9842 |
0．8962 0．9131 0．9278 0．9750 0．9803 0．9846 |
0．8980 0．9147 0．9292 0．9756 0．9808 0．9850 |
0．8997 0．9162 0．9306 0．9762 0．9812 0．9854 |
0．9015 0．9177 0．9319 0．9767 0．9817 0．9857 |
设函数
（Ⅰ）求不等式
的解集
（Ⅱ）求函数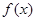
的最小值
已知m，n为正整数.
（Ⅰ）用数学归纳法证明：当x>-1时，
；
（Ⅱ）对于n≥6，已知
，求证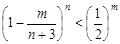
，m=1,1,2…，n；
（Ⅲ）求出满足等式
的所有正整数n.
已知a为给定的正实数，m为实数，函数
．
（Ⅰ）若f（x）在（0，3）上无极值点，求m的值；
（Ⅱ）若存在x0∈（0，3），使得f（x0）是f（x）在[0，3]上的最值，求m的取值范围．
过四面体
的底面上任一点O分别作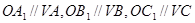
，
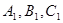分别是所作直线与侧面交点。
求证：
为定值，并求出此定值。
已知函数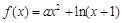
．
（1）当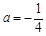
时，求函数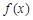
的单调区间；
（2）当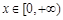
时，不等式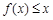
恒成立，求实数
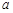的取值范围．
（3）求证：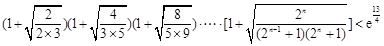
（其中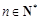
， e是自然对数的底数）．