已知A、B、C是椭圆W: 上的三个点,O是坐标原点.
上的三个点,O是坐标原点.
(I)当点B是W的右顶点,且四边形OABC为菱形时,求此菱形的面积;
(II)当点B不是W的顶点时,判断四边形OABC是否可能为菱形,并说明理由。
已知函数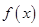 满足如下条件:当
满足如下条件:当 时,
时,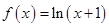 ,且对任
,且对任
意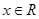 ,都有
,都有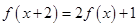 .
.
(1)求函数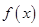 的图象在点
的图象在点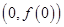 处的切线方程;
处的切线方程;
(2)求当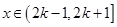 ,
,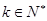 时,函数
时,函数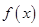 的解析式;
的解析式;
(3)是否存在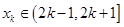 ,
,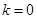 、
、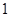 、
、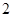 、
、 、
、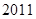 ,使得等式
,使得等式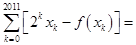
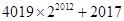 成立?若存在就求出
成立?若存在就求出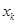 (
(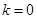 、
、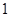 、
、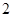 、
、 、
、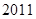 ),若不存在,说明理由.
),若不存在,说明理由.
已知定点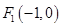 、
、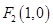 ,动点
,动点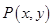 ,且满足
,且满足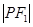 、
、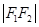 、
、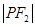
成等差数列.
(1)求点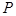 的轨迹
的轨迹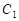 的方程;
的方程;
(2)若曲线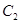 的方程为
的方程为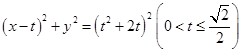 ,过点
,过点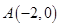 的直线
的直线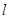 与曲线
与曲线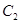 相切,
相切,
求直线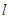 被曲线
被曲线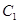 截得的线段长的最小值.
截得的线段长的最小值.
设数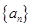 满足:
满足: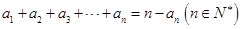 .
.
(1)求证:数列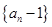 是等比数列;
是等比数列;
(2)若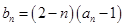 ,且对任意的正整数
,且对任意的正整数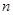 ,都有
,都有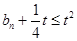 ,求实数
,求实数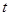 的取值范围.
的取值范围.
如图,在四棱锥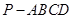 中,底面
中,底面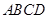 是边长为
是边长为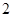 的正方形,侧面
的正方形,侧面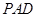
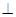
底面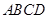 ,且
,且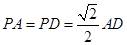 ,
,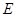 、
、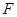 分别为
分别为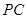 、
、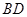 的中点.
的中点.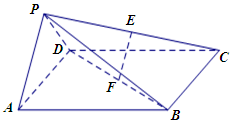
(1)求证: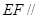 平面
平面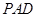 ;
;
(2)求证:面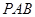
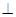 平面
平面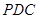 ;
;
(3)在线段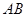 上是否存在点
上是否存在点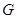 ,使得二面角
,使得二面角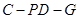 的余弦值为
的余弦值为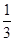 ?说明理由.
?说明理由.
地为绿化环境,移栽了银杏树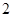 棵,梧桐树
棵,梧桐树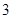 棵.它们移栽后的成活率分别
棵.它们移栽后的成活率分别
为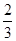 、
、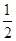 ,每棵树是否存活互不影响,在移栽的
,每棵树是否存活互不影响,在移栽的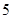 棵树中:
棵树中:
(1)求银杏树都成活且梧桐树成活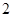 棵的概率;
棵的概率;
(2)求成活的棵树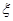 的分布列与期望.
的分布列与期望.