(本小题满分12分)国家教育部要求高中阶段每学年都要组织学生进行“国家学生体质健康数据测试”,方案要求以学校为单位组织实施,某校对高一1班同学按照“国家学生体质健康数据测试”项目按百分制进行了测试,并对50分以上的成绩进行统计,其频率分布直方图如图所示,若90~100分数段的人数为2人.
(Ⅰ)请求出70~80分数段的人数;
(Ⅱ)现根据测试成绩从第一组和第五组(从低分段到高分段依次为第一组、第二组、 、第五组)中任意选出两人,形成搭档小组.若选出的两人成绩差大于20,则称这两人为“搭档组”,试求选出的两人为“搭档组”的概率.
在四棱锥 中,
中,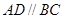 ,
, ,点
,点 是线段
是线段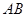 上的一点,且
上的一点,且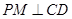 ,
,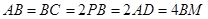 .
.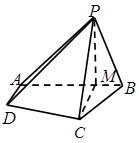
(1)证明:面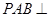 面
面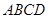 ;
;
(2)求直线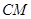 与平面
与平面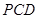 所成角的正弦值.
所成角的正弦值.
如图,海上有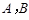 两个小岛相距10
两个小岛相距10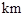 ,船O将保持观望A岛和B岛所成的视角为
,船O将保持观望A岛和B岛所成的视角为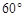 ,现从船O上派下一只小艇沿
,现从船O上派下一只小艇沿 方向驶至
方向驶至 处进行作业,且
处进行作业,且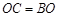 .设
.设
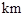 。
。
(1)用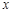 分别表示
分别表示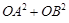 和
和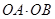 ,并求出
,并求出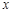 的取值范围;
的取值范围;
(2)晚上小艇在 处发出一道强烈的光线照射A岛,B岛至光线
处发出一道强烈的光线照射A岛,B岛至光线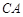 的距离为
的距离为 ,求BD的最大值.
,求BD的最大值.
集合 ,
,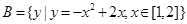 ,若命题
,若命题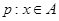 ,命题
,命题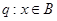 ,且
,且 是
是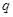 必要不充分条件,求实数
必要不充分条件,求实数 的取值范围。
的取值范围。
(本小题满分14分)已知函数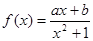 在点
在点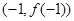 的切线方程为
的切线方程为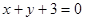 .
.
(Ⅰ)求函数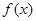 的解析式;
的解析式;
(Ⅱ)设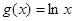 ,求证:
,求证: 在
在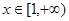 上恒成立;
上恒成立;
(Ⅲ)已知 ,求证:
,求证: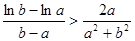 .
.
(本小题满分13分)已知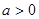 且
且 ,函数
,函数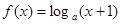 ,
,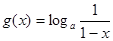 ,记
,记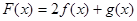 .
.
(Ⅰ)求函数 的定义域
的定义域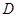 及其零点;
及其零点;
(Ⅱ)若关于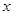 的方程
的方程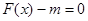 在区间
在区间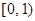 内有解,求实数
内有解,求实数 的取值范围.
的取值范围.