已知数列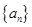 的前
的前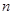 项和为
项和为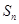 ,且
,且 .
.
(1)求数列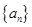 的通项公式;
的通项公式;
(2)若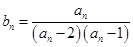 ,数列
,数列 的前
的前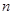 项和为
项和为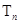 ,证明:
,证明: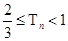 .
.
(本小题满分12分)
如图某市现有自市中心O通往正西和北偏东30°方向的两条主要公路,为了解决该市交通拥挤问题,市政府决定修建一条环城公路.分别在通往正西和北偏东30°方向的公路上选用A、B两点,使环城公路在A、B间为直线段,要求AB路段与市中心O的距离为10 km,且使A、B间的距离|AB|最小.请你确定A、B两点的最佳位置.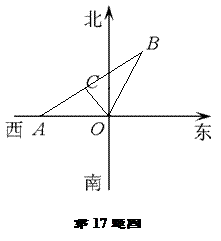
(本小题满分12分)
如图,设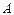 是单位圆和
是单位圆和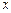 轴正半轴的交点,
轴正半轴的交点,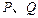 是单位圆上的两点,
是单位圆上的两点, 是
是
坐标原点,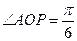 ,
,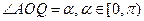 .
.
(1)若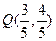 ,求
,求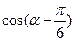 的值;
的值;
(2)设函数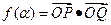 ,求
,求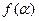 的值域.
的值域.
(本小题满分14分)已知二次函数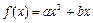 的图像过点
的图像过点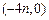 ,且
,且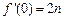 ,
, .
.
(1)若数列 满足
满足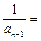
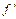
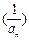 ,且
,且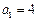 ,求数列
,求数列 的通项公式;
的通项公式;
(2)若数列 满足:
满足: 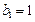 ,
,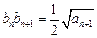 ,当
,当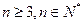 时,
时,
求证:①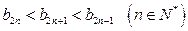 ②
②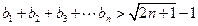
(本小题满分14分)在周长为定值的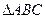 中,已知
中,已知 ,动点
,动点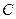 的运动轨迹为曲线G,且当动点
的运动轨迹为曲线G,且当动点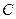 运动时,
运动时,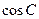 有最小值
有最小值 .
.
(1)以 所在直线为
所在直线为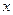 轴,线段
轴,线段 的中垂线为
的中垂线为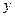 轴建立直角坐标系,求曲线G的方程.
轴建立直角坐标系,求曲线G的方程.
(2)过点(m,0)作圆x2+y2=1的切线l交曲线G于M,N两点.将线段MN的长|MN|表示为m的函数,并求|MN|的最大值.
(本小题满分14分)已知函数 .
.
(1)求函数 的单调区间;
的单调区间;
(2)若以函数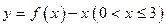 图像上任意一点
图像上任意一点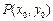 为切点的切线的斜率
为切点的切线的斜率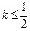 恒成立,求实数a的最小值;
恒成立,求实数a的最小值;