(本小题满分12分)如图,四棱锥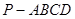 中,
中,
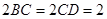 ,侧面APD为等腰直角三角形,
,侧面APD为等腰直角三角形,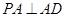 ,平面
,平面 底面
底面 ,
, 为侧棱
为侧棱 上不同于端点的一点.
上不同于端点的一点.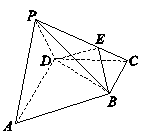
(1)证明: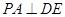 ;
;
(2)试确定点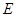 的位置,使二面角
的位置,使二面角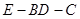 的余弦值为
的余弦值为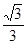 .
.
人寿保险中(某一年龄段),在一年的保险期内,每个被保险人需交纳保费a元,被保险人意外死亡则保险公司赔付3万元,出现非意外死亡则赔付1万元.经统计此年龄段一年内意外死亡的概率是p1,非意外死亡的概率为p2,则a需满足什么条件,保险公司才可能盈利?
设ξ是一个离散型随机变量,其分布列如下表,试求Eξ、Dξ.
| ξ |
-1 |
0 |
1 |
| P |
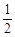 |
1-2q |
q2 |
有甲乙两个箱子,甲箱中有6个小球,其中1个标记0号,2个小球标记1号,3个小球标记2号;乙箱装有7个小球,其中4个小球标记0号,一个标记1号,2个标记2号。从甲箱中取一个小球,从乙箱中取2个小球,一共取出3个小球。求:
(1)取出的3个小球都是0号的概率;
(2)取出的3个小球号码之积是4的概率;
某厂生产电子元件,其产品的次品率为5%,现从一批产品中的任意连续取出2件,求次品数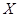 的概率分布
的概率分布
某一射手射击所得环数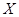 分布列为
分布列为
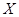 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
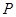 |
0.02 |
0.04 |
0.06 |
0.09 |
0.28 |
0.29 |
0.22 |
求此射手“射击一次命中环数≥7”的概率