(本小题满分12分)已知圆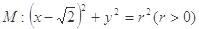 ,若椭圆
,若椭圆 的右顶点为圆
的右顶点为圆 的圆心,离心率为
的圆心,离心率为 .
.
(1)求椭圆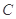 的方程;
的方程;
(2)若存在直线l:y=kx,使得直线 与椭圆
与椭圆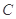 分别交于
分别交于 两点,与圆
两点,与圆 分别交于
分别交于 两点,点
两点,点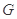 在线段
在线段 上,且
上,且 ,求圆M的半径r的取值范围.
,求圆M的半径r的取值范围.
已知函数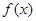 是定义在
是定义在 上的奇函数,且
上的奇函数,且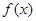 在定义域上是减函数,
在定义域上是减函数,
(1)求函数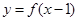 定义域;(2)若
定义域;(2)若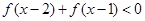 ,求
,求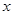 的取值范围.
的取值范围.
已知函数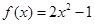 .
.
(1)用定义证明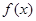 是偶函数;
是偶函数;
(2)用定义证明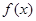 在
在 上是减函数;
上是减函数;
(3)作出函数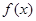 的图像,并写出函数
的图像,并写出函数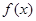 当
当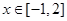 时的最大值与最小值.
时的最大值与最小值.
已知集合A=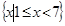 ,B={x|2<x<10},C={x|x<a},全集为实数集R.
,B={x|2<x<10},C={x|x<a},全集为实数集R.
(1)求A∪B, ; (2)如果A∩C≠φ,求a的取值范围.
; (2)如果A∩C≠φ,求a的取值范围.
计算:
(1)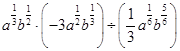 ,
,
(2)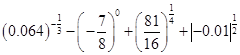
(本小题满分14分)定义在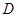 上的函数
上的函数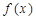 ,如果满足:对任意
,如果满足:对任意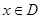 ,存在常数
,存在常数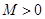 ,都有
,都有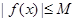 成立,则称
成立,则称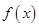 是
是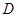 上的有界函数,其中
上的有界函数,其中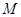 称为函数
称为函数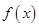 的上界.
的上界.
已知函数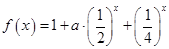 ;
;
(1)当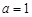 时,求函数
时,求函数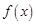 在
在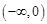 上的值域,并判断函数
上的值域,并判断函数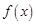 在
在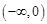 上是否为有界函数,请说明理由;
上是否为有界函数,请说明理由;
(2)若函数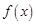 在
在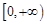 上是以3为上界的有界函数,求实数
上是以3为上界的有界函数,求实数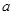 的取值范围
的取值范围