(本小题满分12分)己知函数 ,其中
,其中
(1)求函数 的单调区间;
的单调区间;
(2)若直线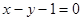 是曲线y=
是曲线y= 的切线,求实数
的切线,求实数 的值;
的值;
(3)设 ,求
,求 在区间
在区间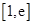 上的最大值(其中e为自然对数的底数)
上的最大值(其中e为自然对数的底数)
一个袋中有大小相同的标有1,2,3,4,5,6的6个小球,某人做如下游戏,每次从
袋中拿一个球(拿后放回),记下标号.若拿出球的标号是3的倍数,则得1分,否则得 分.(Ⅰ)求拿4次至少得2分的概率; (Ⅱ)求拿4次所得分数
分.(Ⅰ)求拿4次至少得2分的概率; (Ⅱ)求拿4次所得分数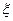 的分布列和数学期望.
的分布列和数学期望.
如图,三棱锥 中,
中,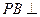 底面
底面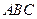 ,
,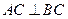 ,
, ,点
,点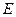 、
、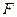 分别是
分别是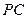 、
、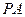 的中点.
的中点.
(Ⅰ)求证: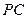 ⊥平面
⊥平面 ;(Ⅱ)求二面角
;(Ⅱ)求二面角 的大小.
的大小.

(本小题满分12分)在 中,已知内角A、B、C所对的边分别为a、b、c,向量
中,已知内角A、B、C所对的边分别为a、b、c,向量 ,
,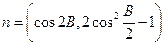 ,且
,且 。(I)求锐角B的大小;(II)如果
。(I)求锐角B的大小;(II)如果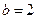 ,求
,求 的面积
的面积 的最大值。
的最大值。
(本小题满分14分)已知递增数列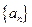 满足:
满足: ,
,
 ,且
,且 、
、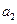 、
、 成等比数列。(I)求数列
成等比数列。(I)求数列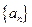 的通项公式
的通项公式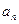 ;(II)若数列
;(II)若数列 满足:
满足: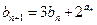
 ,且
,且 。①证明数列
。①证明数列 是等比数列,并求数列
是等比数列,并求数列 的通项公式
的通项公式 ;②设
;②设 ,数列
,数列 前
前 项和为
项和为 ,
,
 ,
, 。当
。当 时,试比较A与B的大小。
时,试比较A与B的大小。