(本小题满分10分)选修4-1:几何证明选讲
如图,AB是圆O的一条切线,切点为B,直线ADE,CFD,CGE,都是圆O的割线,已知AC=AB..
(1)求证: ;
;
(2)若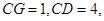 求
求 的值.
的值.
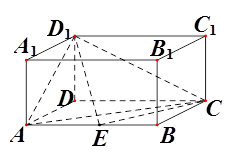
(本小题满分12分)在如图的长方体中,AD=AA1=1,AB=2,点E在棱AB上移动.
(1)当E为AB的中点时,求点E到平面ACD1的距离;
(2)AE等于何值时,二面 角D1-EC-D的大小为
角D1-EC-D的大小为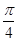 .
.
(本小题满分12分)已知双曲线 的左、右顶点分别为
的左、右顶点分别为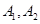 ,点
,点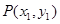 ,
, 是双曲线上不同的两个动点.
是双曲线上不同的两个动点.
(1)求直线 与
与 交点的轨迹E的方程
交点的轨迹E的方程
(2)若过点H(0, h)(h>1)的两条直线 和
和 与轨迹E
与轨迹E 都只有一个公共点,且
都只有一个公共点,且 ,求
,求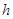 的值.
的值.
(本小题满分12分)已知定义在正实数集上的函数 ,
, ,其中
,其中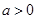 .设两曲线
.设两曲线 ,
, 有公共点,且在该点处的切线相同.
有公共点,且在该点处的切线相同.
(1)用 表示
表示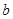 ,并求
,并求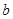 的最大值;
的最大值;
(2)求证: (
( ).
).
(本小题满分10分)已知直线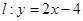 被抛物线C:
被抛物线C: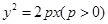 截得的弦长
截得的弦长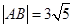 .
.
(1)求抛物线C的方程;
(2)若抛物线C的焦点为F,求三角形ABF的面积.
.已知函数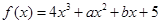 的图像在
的图像在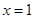 处的切线方程为
处的切线方程为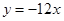 ;
;
(1)求函数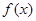 的解析式;
的解析式;
(2)求函数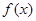 在
在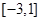 上的最值.
上的最值.