某市现有居民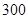 万人,每天有
万人,每天有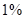 的人选择乘出租车出行,记每个人的乘车里程为
的人选择乘出租车出行,记每个人的乘车里程为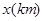 ,
,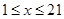 。由调查数据得到
。由调查数据得到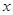 的频率分布直方图(如图)。在直方图的乘车里程分组中,可以用各组的区间中点值代表该组的各个值,乘车里程落人该区间的频率作为乘车里程取区间中点值得概率。现规定乘车里程
的频率分布直方图(如图)。在直方图的乘车里程分组中,可以用各组的区间中点值代表该组的各个值,乘车里程落人该区间的频率作为乘车里程取区间中点值得概率。现规定乘车里程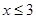 时,乘车费用为
时,乘车费用为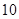 元;当
元;当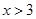 时,每超出
时,每超出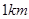 (不足
(不足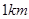 时按
时按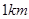 计算),乘车费用增加
计算),乘车费用增加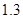 元。
元。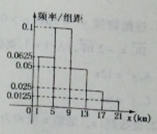
(Ⅰ)求从乘客中任选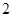 人乘车里程相差超过
人乘车里程相差超过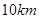 的概率;
的概率;
(Ⅱ)试估计出租车公司一天的总收入是多小?(精确到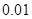 万元)
万元)
若某几何体的三视图(单位:cm)如图所示,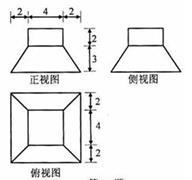
(Ⅰ)求此几何体的表面积;
(Ⅱ)求此几何体的体积.
已知圆 的圆心
的圆心 在
在 轴上,半径为2,直线
轴上,半径为2,直线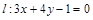 被圆
被圆 截得的弦长为
截得的弦长为 ,且圆心
,且圆心 在直线
在直线 的上方.
的上方.
(1)求圆 的方程;
的方程;
(2)设 ,
,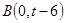 (2≤t≤4),若圆
(2≤t≤4),若圆 是
是 的内切圆,求
的内切圆,求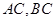 边所在直线的斜率(用
边所在直线的斜率(用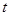 表示)
表示)
(3)在(2)的条件下求 的面积S的最大值及对应的
的面积S的最大值及对应的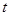 值.
值.
记事件A为“直线 与圆
与圆 相交”
相交”
(1)若将一颗骰子先后掷两次得到的点数分别记为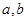 ,求事件A发生的概率
,求事件A发生的概率
(2)若实数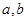 满足
满足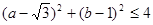 ,求事件A发生的概率.
,求事件A发生的概率.
已知 的顶点
的顶点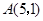 ,
,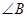 的内角平分线BN所在直线方程为
的内角平分线BN所在直线方程为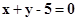 ,
, 边上的中线
边上的中线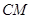 所在直线方程为
所在直线方程为 .
.
求:(1)顶点B的坐标;
(2)直线BC方程.
从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量表得如下频数分布表:
| 质量指标值分组 |
[75,85) |
[85,95) |
[95,105) |
[105,115) |
[115,125) |
| 频数 |
6 |
26 |
38 |
22 |
8 |
(1)在答题卡上作出这些数据的频率分布直方图 (用阴影表示)
(2)估计这种产品质量指标值的平均数及中位数
(3)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品的80%”的规定?