（本小题满分7分）《选修4-4：坐标系与参数方程》
在极坐标系中，圆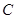
的极坐标方程为
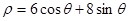．现以极点
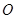为原点，极轴为
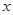轴的非负半轴建立平面直角坐标系．
（Ⅰ）求圆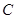的直角坐标方程；
（Ⅱ）若圆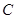上的动点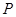
的直角坐标为
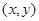，求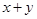
的最大值，并写出
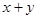取得最大值时点P的直角坐标．
（本小题满分14分）已知函数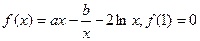
．
（Ⅰ）若函数f(x)在其定义域内为单调函数，求a的取值范围；
（Ⅱ）若函数f(x)的图象在x = 1处的切线的斜率为0，且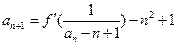
，已
知a1 = 4，求证：an³ 2n + 2；
（Ⅲ）在（Ⅱ）的条件下，试比较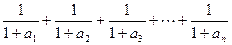
与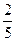
的大小，并说明你的理由．
（本小题满分13分）
定长为3的线段AB两端点A、B分别在
轴，
轴上滑动，M在线段AB上，且
（1）求点M的轨迹C的方程；
（2）设过
且不垂直于坐标轴的动直线
交轨迹C于A、B两点，问：线段
上
是否存在一点D，使得以DA，DB为邻边的平行四边形为菱形？作出判断并证明。
（本小题满分12分）已知函数
（1）求函数
的最大值；
（2）当
时，求证
；
（本小题满分12分）
已知适合不等式
的x的最大值为3，求p的值。
（本小题满分12分）如图，在四棱锥P—ABCD中，底面
ABCD为矩形，侧棱PA⊥底面ABCD，AB=，BC=1，PA=2，E为PD的中点．
（1）求直线AC与PB所成角的余弦值；
（2）在侧面PAB内找一点N，使NE⊥面PAC，并求出N点到AB和AP的距离．