(本小题满分14分)已知 ,函数
,函数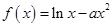 ,
, .(
.( 的图象连续不断)
的图象连续不断)
(Ⅰ) 求 的单调区间;
的单调区间;
(Ⅱ) 当 时,证明:存在
时,证明:存在 ,使
,使 ;
;
(Ⅲ) 若存在属于区间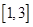 的
的 ,且
,且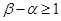 ,使
,使 ,证明:
,证明: .
.
已知函数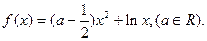
(Ⅰ)当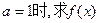 在区间
在区间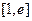 上的最大值和最小值;
上的最大值和最小值;
(Ⅱ)若在区间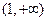 上,函数
上,函数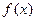 的图象恒在直线
的图象恒在直线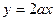 下方,求
下方,求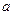 的取值范围.
的取值范围.
在棱长为2的正方体ABCD—A1B1C1D1中,E,F分别为A1D1和CC1的中点.
(Ⅰ)求证:EF//平面ACD1;
(Ⅱ)求异面直线EF与AB所成的角的余弦值;
(Ⅲ)在棱BB1上是否存在一点P,使得二面角P—AC—B的大小为30°?若存在,求出BP的长;若不存在,请说明理由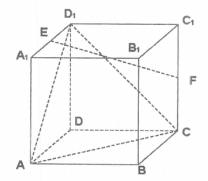
为增强市民的节能环保意识,某市面向全市征召义务宣传志愿者,从符合条件的500名志愿者中随机抽样100名志原者的年龄情况如下表所示。
(Ⅰ)频率分布表中的①、②位置应填什么数据?并在答题卡中补全频率分布直方图(如图),再根据频率分布直方图估计这500名志愿者中年龄在 岁的人数;
岁的人数;
(Ⅱ)在抽出的100名志原者中按年龄再采用分层抽样法抽取20人参加中心广场的宣传活动,从这20人中选取2名志愿者担任主要负责人,记这2名志愿者中“年龄低于30岁”的人数为X,求X的分布列及数学期望。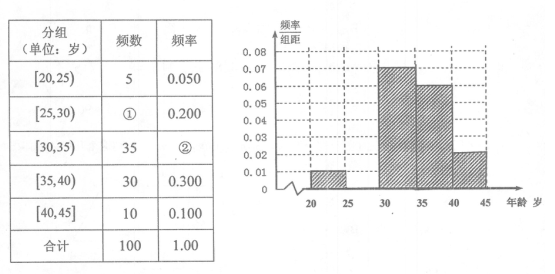
在 中,角A,B,C所对应的边分别为
中,角A,B,C所对应的边分别为
(Ⅰ)求角C的大小;
(Ⅱ)求 的最大值.
的最大值.
已知数列{an},且x= 是函数f(x)=an-1x3-3[(t+1)an-an+1] x+1(n≥2)的
是函数f(x)=an-1x3-3[(t+1)an-an+1] x+1(n≥2)的 一个极值点.数列{an}中a1=t,a2=t2(t>0且t≠1) .
一个极值点.数列{an}中a1=t,a2=t2(t>0且t≠1) .
(1)求数列{an}的通项公式;
(2)记bn=2(1-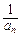 ),当t=2时,数列{bn}的前n项和为Sn,求使Sn>2010的n的最小值;
),当t=2时,数列{bn}的前n项和为Sn,求使Sn>2010的n的最小值;
(3)若cn=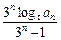 ,证明:
,证明: ( n∈N﹡).
( n∈N﹡).