【改编】(本小题满分14分)已知函数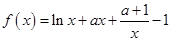 .
.
(1)若函数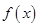 在
在 处有极值,求
处有极值,求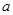 的值;
的值;
(2)当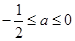 时,讨论
时,讨论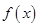 的单调性.
的单调性.
已知函数f(x)=ax+lnx,其中a为常数,设e为自然对数的底数.
(Ⅰ) 当a=-1时,求f(x)的最大值;
(Ⅱ) 若f(x)在区间(0,e]上的最大值为-3,求a的值;
(Ⅲ) 当a=-1时,试推断方程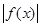 =
=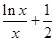 是否有实数解.
是否有实数解.
已知椭圆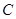 :
: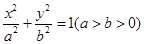 的离心率为
的离心率为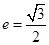 ,且过点
,且过点 .
.
(Ⅰ)求椭圆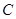 的标准方程;
的标准方程;
(Ⅱ)垂直于坐标轴的直线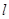 与椭圆
与椭圆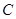 相交于
相交于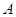 、
、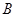 两点,若以
两点,若以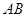 为直径的圆
为直径的圆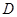 经过坐标原点.证明:圆
经过坐标原点.证明:圆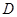 的半径为定值.
的半径为定值.
某大学为调查来自南方和北方的同龄大学生的身高差异,从2011级的年龄在18~19岁之间的大学生中随机抽取了来自南方和北方的大学生各10名,测量他们的身高,量出的身高如下:(单位:cm)
南方:158,170,166,169,180,175,171,176,162,163;
北方:183,173,169,163,179,171,157,175,178,166;
(Ⅰ)根据抽测结果,画出茎叶图,并根据你画的茎叶图,对来自南方和北方的大学生的身高作比较,写出两个统计结论;
(Ⅱ)若将样本频率视为总体的概率,现从来自南方的身高不低于170的大学生中随机抽取3名同学,求其中恰有两名同学的身高低于175的概率.
在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,PA=2AB=2.
(Ⅰ)求四棱锥P-ABCD的体积V;
(Ⅱ)若F为PC的中点,求证PC⊥平面AEF;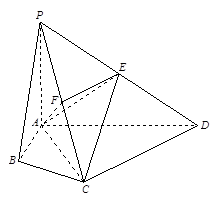
阅读下面材料:
根据两角和与差的正弦公式,有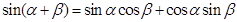 ------①
------①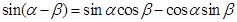 ------②
------②
由①+② 得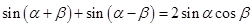 ------③
------③
令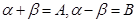 有
有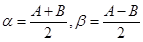
代入③得 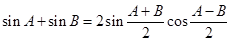 .
.
(Ⅰ) 类比上述推理方法,根据两角和与差的余弦公式,证明: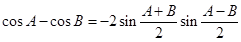 ;
;
(Ⅱ)若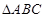 的三个内角
的三个内角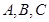 满足
满足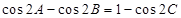 ,试判断
,试判断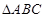 的形状.
的形状.
(提示:如果需要,也可以直接利用阅读材料及(Ⅰ)中的结论)