(本小题满分12分)某校在一次对学生在课外活动中喜欢跑步和喜欢打球的学生的抽样调查
中,随机抽取了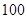 名同学,相关数据如下表所示:
名同学,相关数据如下表所示:
| |
喜欢跑步 |
喜欢打球 |
总计 |
| 男生 |
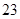 |
 |
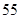 |
| 女生 |
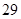 |
 |
 |
| 总计 |
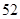 |
 |
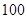 |
(1)由表中数据直观分析,喜欢打球的学生是否与性别有关?
(2)用分层抽样的方法在喜欢打球的学生中随机抽取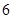 名,求男学生应该抽取几名?
名,求男学生应该抽取几名?
(3)在上述抽取的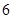 名学生中任取
名学生中任取 名,求恰有
名,求恰有 名女学生的概率.
名女学生的概率.
如图,在棱长为2的正方体 中,
中, 分别是棱
分别是棱 的中点,点
的中点,点 分别在棱
分别在棱 ,
, 上移动,且
上移动,且 .
.
(1)当 时,证明:直线
时,证明:直线
 平面
平面 ;
;
(2)
是否存在 ,使平面
,使平面 与面
与面 所成的二面角为直二面角?若存在,求出
所成的二面角为直二面角?若存在,求出 的值;若不存在,说明理由.
的值;若不存在,说明理由.
如图,四边形 为正方形,
为正方形, 平面
平面 ,
, ,
, 于点
于点 ,
, ,交
,交 于点
于点 .
.
(1)证明:
(2)求二面角 的余弦值。
的余弦值。
如图,正方形 的边长为2,
的边长为2, 分别为
分别为 的中点,在五棱锥
的中点,在五棱锥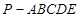 中,
中, 为棱
为棱 的中点,平面
的中点,平面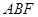 与棱
与棱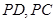 分别交于点
分别交于点 .
.
(1)求证: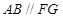 ;
;
(2)若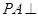 底面
底面 ,且
,且 ,求直线
,求直线 与平面
与平面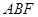 所成角的大小,并求线段
所成角的大小,并求线段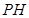 的长.
的长.
如图,在三棱锥P ABC中,D,E,F分别为棱PC,AC,AB的中点。已知PA⊥AC,PA=6,BC=8,DF=5.
ABC中,D,E,F分别为棱PC,AC,AB的中点。已知PA⊥AC,PA=6,BC=8,DF=5.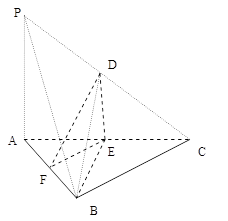
求证:(1)直线PA∥平面DEF;
(2)平面BDE⊥平面ABC.
如图三棱柱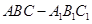 中,侧面
中,侧面 为菱形,
为菱形, .
.
(Ⅰ)证明: ;
;
(Ⅱ)若 ,
,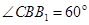 ,AB=BC,求二面角
,AB=BC,求二面角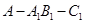 的余弦值.
的余弦值.