(本小题满分14分)如图,在四棱锥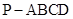 中,底面
中,底面 是正方形,
是正方形,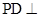 平面
平面 .点
.点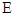 是线段
是线段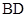 的中点,点
的中点,点 是线段
是线段 上的动点.
上的动点.
(1)若 是
是 的中点,求证:
的中点,求证: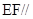 平面
平面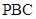 ;
;
(2)求证: ;
;
(3)若 ,
, ,当三棱锥
,当三棱锥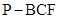 的体积等于
的体积等于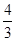 时,试判断点
时,试判断点 在边
在边 上的位置,并说明
上的位置,并说明
理由.
设集合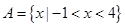 ,
,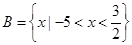 ,
,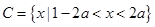 .
.
(Ⅰ)若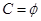 ,求实数
,求实数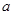 的取值范围;
的取值范围;
(Ⅱ)若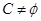 且
且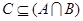 ,求实数
,求实数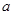 的取值范围.
的取值范围.
(1)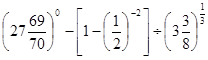
(2)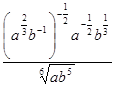
已知函数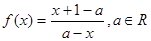 。利用函数
。利用函数 构造一个数列
构造一个数列 ,方法如下:对于定义域中给定的
,方法如下:对于定义域中给定的 ,令
,令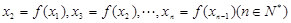 ,…
,…
如果取定义域中任一值作为 ,都可以用上述方法构造出一个无穷数列
,都可以用上述方法构造出一个无穷数列 。
。
(1)求实数a的值;
(2)若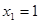 ,求
,求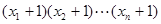 的值;
的值;
(3)设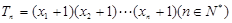 ,试问:是否存在n使得
,试问:是否存在n使得 成立,若存在,试确定n及相应的
成立,若存在,试确定n及相应的 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
已知数列{an}中,a1=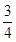 ,an+1=
,an+1= (n∈N*).
(n∈N*).
(1)求证:数列{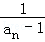 }是等差数列,并求{an}的通项公式;
}是等差数列,并求{an}的通项公式;
(2)设bn+an=l(n∈N*),S=b1b2+b2b3+…+bnbn+1,试比较an与8Sn的大小.
已知向量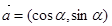 ,
, ,
,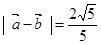 。
。
(1)求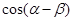 的值;
的值;
(2)若 且
且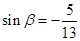 ,求
,求 的值。
的值。