(Ⅰ)如果三段的长度均为整数,求能构成三角形的概率;
(Ⅱ)如果把铁丝截成2,2,3的三段放入一个盒子中,然后有放回地摸4次,设摸到长度为2的次数为 ,求
,求 与
与 ;
;
(Ⅲ)如果截成任意长度的三段,求能构成三角形的概率.
(1)证明二维形式的柯西不等式:
(2)若实数 满足
满足 求
求 的取值范围.
的取值范围.
在极坐标系中,圆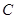 的圆心坐标为
的圆心坐标为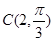 ,半径为2.以极点为原点,极轴为
,半径为2.以极点为原点,极轴为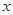 的正半轴,取相同的长度单位建立平面直角坐标系,
的正半轴,取相同的长度单位建立平面直角坐标系,
直线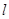 的参数方程为
的参数方程为 (
(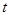 为参数)
为参数)
(1)求圆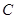 的极坐标方程
的极坐标方程
(2)设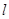 与圆
与圆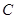 的交点为
的交点为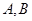 ,
,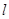 与
与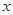 轴的交点为
轴的交点为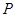 ,求
,求 .
.
如图,矩形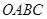 和平行四边形
和平行四边形 的部分顶点坐标为:
的部分顶点坐标为: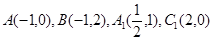 .
.
(1)求将矩形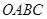 变为平行四边形
变为平行四边形 的线性变换对应的矩阵
的线性变换对应的矩阵 ;
;
(2)矩阵 是否存在特征值?若存在,求出矩阵
是否存在特征值?若存在,求出矩阵 的所有特征值及其对应的一个特征向量;若不存在,请说明理由.
的所有特征值及其对应的一个特征向量;若不存在,请说明理由.
已知函数
 为自然对数的底数).
为自然对数的底数).
(1)求曲线 在
在 处的切线方程;
处的切线方程;
(2)若 是
是 的一个极值点,且点
的一个极值点,且点 ,
, 满足条件:
满足条件:  .
.
(ⅰ)求 的值;
的值;
(ⅱ)若点 , 判断
, 判断 三点是否可以构成直角三角形?请说明理由.
三点是否可以构成直角三角形?请说明理由.
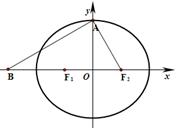
如图,设椭圆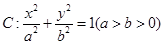 的左右焦点为
的左右焦点为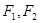 ,上顶点为
,上顶点为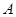 ,点
,点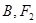 关于
关于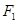 对称,且
对称,且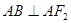
(1)求椭圆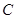 的离心率;
的离心率;
(2)已知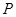 是过
是过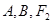 三点的圆上的点,若
三点的圆上的点,若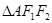 的面积为
的面积为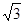 ,求点
,求点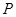 到直线
到直线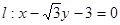 距离的最大值.
距离的最大值.