【改编】(本小题满分14分)已知正项数列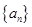 的前
的前 项和为
项和为 ,且
,且 ,
,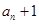 ,
, 成等比数列.
成等比数列.
(1)求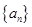 的通项公式;
的通项公式;
(2)设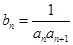 ,求
,求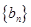 的前
的前 项和
项和 ;
;
(3)在(2)的条件下,对任意 ,
,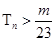 都成立,求整数
都成立,求整数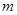 的最大值.
的最大值.
已知函数f(x)=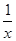 +ln x(a≠0,a∈R).求函数f(x)的极值和单调区间.
+ln x(a≠0,a∈R).求函数f(x)的极值和单调区间.
已知直线 经过点
经过点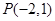 .
.
(1)若直线 的方向向量为
的方向向量为 ,求直线
,求直线 的方程;
的方程;
(2)若直线 在两坐标轴上的截距相等,求此时直线
在两坐标轴上的截距相等,求此时直线 的方程.
的方程.
已知圆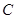 通过不同三点
通过不同三点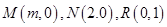 ,且直线
,且直线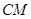 斜率为
斜率为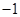 ,
,
(1)试求圆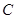 的方程;
的方程;
(2)若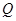 是
是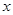 轴上的动点,
轴上的动点, 分别切圆
分别切圆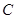 于
于 两点,
两点,
①求证:直线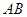 恒过一定点;
恒过一定点;
②求 的最小值.
的最小值.
已知向量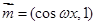 ,
,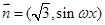 (
(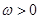 ),函数
),函数 ,且
,且 图象上一个最高点为
图象上一个最高点为
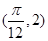 ,与
,与 最近的一个最低点的坐标为
最近的一个最低点的坐标为 .
.
(1)求函数 的解析式;
的解析式;
(2)设 为常数,判断方程
为常数,判断方程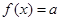 在区间
在区间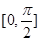 上的解的个数;
上的解的个数;
(3)在锐角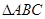 中,若
中,若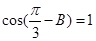 ,求
,求 的取值范围.
的取值范围.
已知定义域为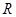 的函数
的函数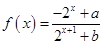 是奇函数,
是奇函数,
(1)求 的值;
的值;
( 2) 判断并证明函数 的单调性;
的单调性;
(3)若对任意的 ,不等式
,不等式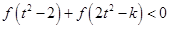 恒成立,求
恒成立,求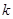 的取值范围.
的取值范围.