某种商品原来每件售价为25元，年销售8万件．
（1）据市场调查，若价格每提高1元，销售量将相应减少2000件，要使销售的总收入不低于原收入，该商品每件定价最多为多少元？
（2）为了扩大该商品的影响力，提高年销售量．公司决定明年对该商品进行全面技术革新和营销策略改革，并提高定价到
元．公司拟投入
万元作为技改费用，投入50万元作为固定宣传费用，投入
万元作为浮动宣传费用．试问：当该商品明年的销售量
至少应达到多少万件时，才可能使明年的销售收入不低于原收入与总投入之和？并求出此时商品的每件定价．
设向量a=(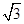
sin x,sin x),b="(cos" x,sin x),x∈
.
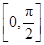(1)若|a|=|b|,求x的值;
(2)设函数f(x)=a·b,求f(x)的最大值.
如图甲，在平面四边形ABCD中，已知∠A＝45°，∠C＝90°，∠ADC＝105°，AB＝BD，现将四边形ABCD沿BD折起，使平面ABD⊥平面BDC(如图乙)，设点E、F分别为棱AC、AD的中点．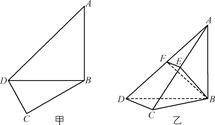
(1)求证：DC⊥平面ABC；
(2)求BF与平面ABC所成角的正弦值；
(3)求二面角B－EF－A的余弦值．
如图，在三棱柱ABCA1B1C1中，A1B⊥平面ABC，AB⊥AC，且AB＝AC＝A1B＝2.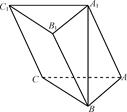
(1)求棱AA1与BC所成的角的大小；
(2)在棱B1C1上确定一点P，使二面角P－AB－A1的平面角的余弦值为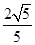
.
三棱柱ABC－A1B1C1在如图所示的空间直角坐标系中，已知AB＝2，AC＝4，A1A＝3.D是BC的中点．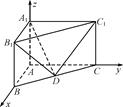
(1)求直线DB1与平面A1C1D所成角的正弦值；
(2)求二面角B1-A1D-C1的正弦值．
在直四棱柱ABCD-A1B1C1D1中，AA1＝2，底面是边长为1的正方形，E、F分别是棱B1B、DA的中点．
(1)求二面角D1-AE-C的大小；
(2)求证：直线BF∥平面AD1E.