（本小题满分12分）某班主任对全班50名学生学习积极性和参加社团活动情况进行调查，统计数据如表1所示
表1
| |
参加社团活动 |
不参加社团活动 |
合计 |
| 学习积极性高 |
17 |
8 |
25 |
| 学习积极性一般 |
5 |
20 |
25 |
| 合计 |
22 |
28 |
50 |
（1）如果随机从该班抽查一名学生，抽到参加社团活动的学生的概率是多少？抽到不参加社团活动且学习积极性一般的学生的概率是多少？
（2）运用独立检验的思想方法分析：学生的学习积极性与参加社团活动情况是否有关系？并说明理由．
 |
0．05 |
0．01 |
0．001 |
 |
3．841 |
6．635 |
10．828 |
选修4﹣2：矩阵与变换
已知二阶矩阵A有特征值λ1=1及对应的一个特征向量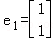
和特征值λ2=2及对应的一个特征向量
，试求矩阵A．
设矩阵A=
，矩阵A属于特征值λ1=﹣1的一个特征向量为α1=
，属于特征值λ2=4的一个特征向量为α2=
，求ad﹣bc的值．
若兔子和狐狸的生态模型为
（n≥1），对初始群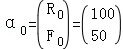
，讨论第n年种群数量αn及当n越来越大时，种群数量αn的变化趋势．
已知二阶矩阵M有特征值λ=8及对应的一个特征向量
=
，并且矩阵M对应的变换将点（﹣1，2）变换成（﹣2，4）．
（1）求矩阵M；
（2）求矩阵M的另一个特征值，及对应的一个特征向量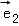
的坐标之间的关系．
（3）求直线l：x﹣y+1=0在矩阵M的作用下的直线l′的方程．
已知矩阵
，若矩阵A属于特征值6的一个特征向量为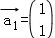
，属于特征值1的一个特征向量为
，求矩阵A．