(本小题满分15分)已知椭圆 的离心率为
的离心率为 ,其左焦点
,其左焦点 到点
到点 的距离为
的距离为 .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)过右焦点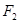 的直线与椭圆交于不同的两点
的直线与椭圆交于不同的两点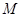 、
、 ,则
,则 内切圆的圆面积是否存在最大值?若存在,求出这个最大值及此时的直线方程;若不存在,请说明理由.
内切圆的圆面积是否存在最大值?若存在,求出这个最大值及此时的直线方程;若不存在,请说明理由.
(本小题共13分)某厂生产的产品在出厂前都要做质量检测,每一件一等品都能通过检测,每一件二等品通过检测的概率为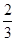 .现有10件产品,其中6件是一等品,4件是二等品.
.现有10件产品,其中6件是一等品,4件是二等品.
(Ⅰ) 随机选取1件产品,求能够通过检测的概率;
(Ⅱ) 随机选取3件产品,其中一等品的件数记为 ,求
,求 的分布列;
的分布列;
(Ⅲ) 随机选取3件产品,求这三件产品都不能通过检测的概率.
(本小题共14分)在如图的多面体中, ⊥平面
⊥平面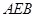 ,
, ,
, ,
, ,
, ,
, ,
,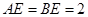 ,
, 是
是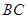 的中点.
的中点.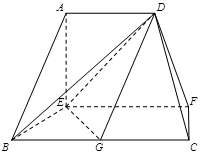
(Ⅰ) 求证: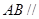 平面
平面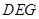 ;
;
(Ⅱ) 求证: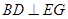 ;
;
(Ⅲ) 求二面角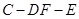 的余弦值.
的余弦值.
(本小题共13分)在 中,内角A、B、C所对的边分别为
中,内角A、B、C所对的边分别为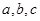 ,已知
,已知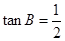 ,
,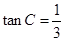 ,且
,且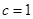 .
.
(Ⅰ)求 ;
;
(Ⅱ)求 的面积.
的面积.
(本小题满分14分)设函数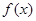 的定义域为R,当
的定义域为R,当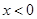 时,
时,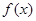
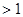 ,且对任意的实数
,且对任意的实数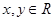 ,有
,有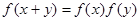 .
.
(1)求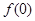 ,判断并证明函数
,判断并证明函数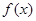 的单调性;
的单调性;
(2)数列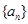 满足
满足 ,且
,且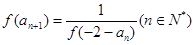
①求 的通项公式;
的通项公式;
②当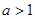 时,不等式
时,不等式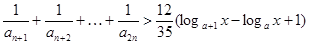 对不小于2的正整数
对不小于2的正整数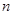 恒成立,求
恒成立,求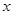 的取值范围.
的取值范围.
(本小题满分14分)已知函数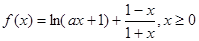 ,其中
,其中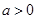
(Ⅰ)求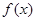 的单调区间;
的单调区间;
(Ⅱ)若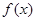 的最小值为1,求
的最小值为1,求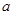 的取值范围.
的取值范围.